Skip to contents

Moran's I test for spatial autocorrelation

Source: R/moran.R
moran.Rd

Computes Moran's I, a measure of spatial autocorrelation that tests whether values are more similar (positive autocorrelation) or dissimilar (negative autocorrelation) among spatial neighbors than expected by chance.

Usage

moran(
  x = NULL,
  distance.matrix = NULL,
  distance.threshold = NULL,
  verbose = TRUE
)

Arguments

x

Numeric vector to test for spatial autocorrelation. Typically model residuals or a response variable.

distance.matrix

Numeric distance matrix between observations. Must have the same number of rows as the length of x.

distance.threshold

Numeric value specifying the maximum distance for spatial neighbors. Distances above this threshold are set to zero during weighting. Default: NULL (automatically set to 0, meaning no thresholding).

verbose

Logical. If TRUE, displays a Moran's scatterplot. Default: TRUE.

Value

List of class "moran" with three elements:

  • test: Data frame containing:

    • distance.threshold: The distance threshold used

    • moran.i.null: Expected Moran's I under null hypothesis of no spatial autocorrelation

    • moran.i: Observed Moran's I statistic

    • p.value: Two-tailed p-value from normal approximation

    • interpretation: Text interpretation of the result

  • plot: ggplot object showing Moran's scatterplot (values vs. spatial lag values with linear fit).

  • plot.df: Data frame with columns x (original values) and x.lag (spatially lagged values) used to generate the plot.

Details

Moran's I is a measure of spatial autocorrelation that quantifies the degree to which nearby observations have similar values. The statistic ranges approximately from -1 to +1:

  • Positive values: Similar values cluster together (positive spatial autocorrelation)

  • Values near zero: Random spatial pattern (no spatial autocorrelation)

  • Negative values: Dissimilar values are adjacent (negative spatial autocorrelation, rare in practice)

Statistical testing:

The function compares the observed Moran's I to the expected value under the null hypothesis of no spatial autocorrelation (EI = -1/(n-1)). The p-value is computed using a normal approximation. Results are interpreted at 0.05 significance level.

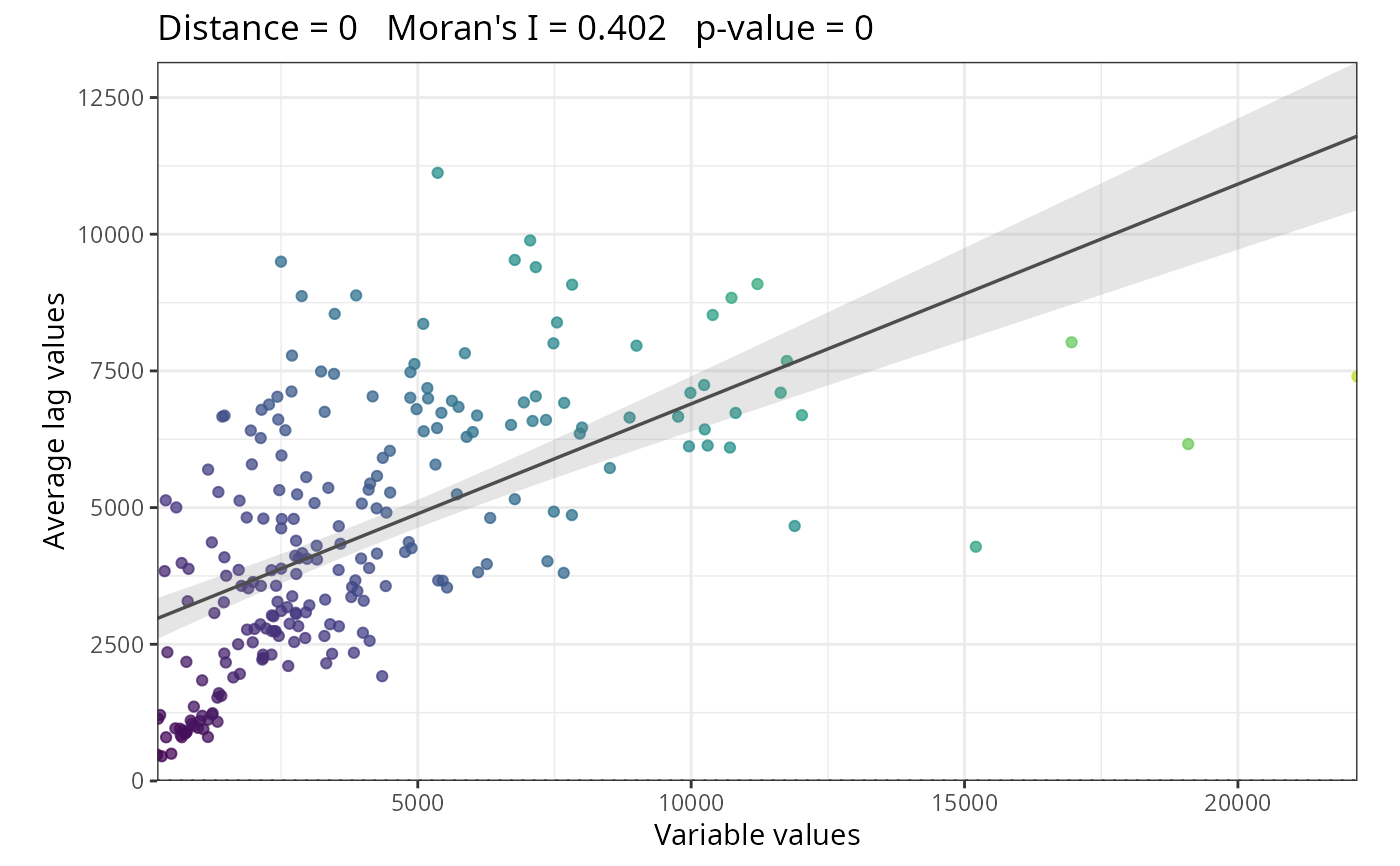
Moran's scatterplot:

The plot shows original values (x-axis) against spatially lagged values (y-axis). The slope of the fitted line approximates Moran's I. Points in quadrants I and III indicate positive spatial autocorrelation; points in quadrants II and IV indicate negative spatial autocorrelation.

This implementation is inspired by the Moran.I() function in the ape package.

See also

moran_multithreshold(), get_moran()

Other spatial_analysis: filter_spatial_predictors(), mem(), mem_multithreshold(), moran_multithreshold(), pca(), pca_multithreshold(), rank_spatial_predictors(), residuals_diagnostics(), residuals_test(), select_spatial_predictors_recursive(), select_spatial_predictors_sequential()

Examples

data(plants_df, plants_distance, plants_response)

# Test for spatial autocorrelation in response variable
moran_test <- moran(
  x = plants_df[[plants_response]],
  distance.matrix = plants_distance,
  distance.threshold = 1000
)


# View test results
moran_test$test
#>   distance.threshold moran.i.null   moran.i p.value
#> 1               1000 -0.004424779 0.2588432       0
#>                 interpretation
#> 1 Positive spatial correlation

# Access components
moran_test$test$moran.i  # Observed Moran's I
#> [1] 0.2588432
moran_test$test$p.value  # P-value
#> [1] 0
moran_test$test$interpretation  # Text interpretation
#> [1] "Positive spatial correlation"