Skip to contents

Getting Started

getting_started.Rmd

This article walks through the complete memoria workflow for quantifying ecological memory in time series data consisting of at least one response and one predictor.

Ecological Memory

The package memoria helps quantify how past and concurrent events shape the state of a system. This concept is summarized in the figure below:

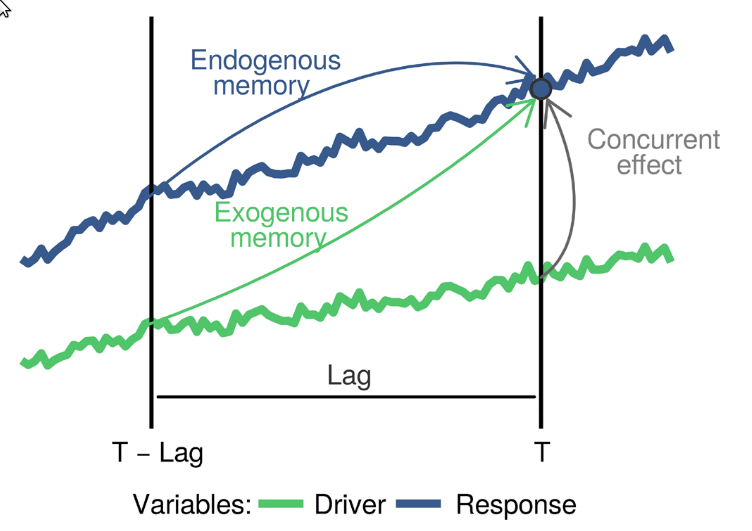Ecological Memory The blue and green curves represent the values of a biotic response y and a driver x over time. The vertical line T represents the current time, while T - lag represents a previous time. The arrows represent influence, as follows:

  • Endogenous memory: is the effect of past y on present y.
  • Exogenous memory: is the effect of past x on present y.
  • Concurrent effect: is the effect of present x on present y.

To assess these effects, memoria generates the lagged data and trains the model

yT=yT−1+…+yT−n+xT+xT−1+…+xT−n+rTy_{T} = y_{T-1} + \ldots + y_{T-n} + x_{T} + x_{T-1} + \ldots + x_{T-n} + r_{T}

Where:

  • yy and xx are the response and the driver.
  • TT is the “current” time, and T−1T-1 to T−nT-n, are the time lags.
  • yT−1+…+yT−ny_{T-1} + \ldots + y_{T-n} represents the endogenous memory across lags.
  • xT−1+…+xT−nx_{T-1} + \ldots + x_{T-n} represents the exogenous memory across lags.
  • xTx_{T} represents the concurrent effect.
  • rTr_{T} is a random term used to assess statistical significance.

The ecological memory pattern is quantified using permutation importance from Random Forest models. For each predictor, the algorithm shuffles its values and measures the decrease in predictive accuracy. Larger decreases indicate stronger influence on the response.

To visualize ecological memory, the package memoria plots permutation importance scores across time lags.

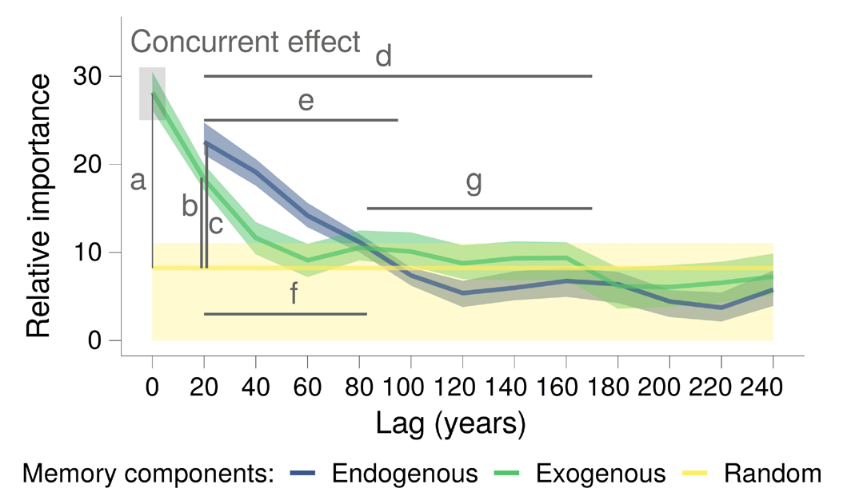
Ecological Memory
Ecological Memory

Where:

  • a: strength of the concurrent effect (highlighted by a grey box).
  • b and c: strength of the exogenous and endogenous memory.
  • d and e: length of the exogenous and endogenous memory.
  • f and g: dominance across lags of the endogenous and exogenous memory.

The following sections demonstrate how to implement this workflow in R using the memoria package.

Setup

Workflow

The typical workflow involves time series with one response variable and one or several drivers.

The package memoria has two example datasets, one with responses and one with drivers:

  • pollen: irregular time series with 639 samples and four pollen types (Pinus, Quercus, Poaceae, Artemisia).
data(pollen, package = "memoria")

pollen |> 
  distantia::tsl_init(
    time_column = "age"
  ) |> 
  distantia::tsl_plot(
    ylim = "relative",
    guide = FALSE
  )

  • climate: regular time series with 800 samples taken every 1000 years, with climate variables (temperature, rainfall, etc.)
data(climate, package = "memoria")

climate |> 
  distantia::tsl_init(
    time_column = "age"
  ) |> 
  distantia::tsl_plot(
    ylim = "relative",
    guide = FALSE,
    line_color = "blue4"
  )

Align Datasets

The package memoria requires the input time series to be regular, but pollen is irregular, with a range of time intervals between 0.32 and 6.475.

To homogenize both datasets, below we use linear interpolation with time to align pollen with climate.

df <- memoria::alignTimeSeries(
  datasets.list = list(
    pollen = pollen,
    climate = climate
  ),
  time.column = "age",
  interpolation.interval = 1
)

nrow(df)
#> [1] 799
range(diff(df$age)) #1000 years
#> [1] 1 1
colnames(df)
#>  [1] "age"                             "pollen.pinus"                   
#>  [3] "pollen.quercus"                  "pollen.poaceae"                 
#>  [5] "pollen.artemisia"                "climate.temperatureAverage"     
#>  [7] "climate.rainfallAverage"         "climate.temperatureWarmestMonth"
#>  [9] "climate.temperatureColdestMonth" "climate.oxigenIsotope"

Now that the responses and the drivers are at the same resolution, we just need to select the data we want to play with.

df <- df |> 
  dplyr::transmute(
    time = age,
    quercus = pollen.quercus,
    rain = climate.rainfallAverage,
    temp = climate.temperatureAverage
  )

Create lagged data

The lagTimeSeries() function organizes data into the lag structure required by the model. Each sample of the response is aligned with antecedent values of itself and the drivers. In this case we use lags 1 to 10, which correspond with 1000 to 10000 years.

quercus_lags <- lagTimeSeries(
  input.data = df,
  response = "quercus",
  drivers = c("rain", "temp"),
  time = "time",
  oldest.sample = "last",
  lags = seq(from = 1, to = 10, by = 1)
)

Note on oldest.sample: Set to "last" when the oldest sample is at the bottom of the dataframe (typical palaeoecological convention). Set to "first" if the oldest sample is at the top.

The output columns follow a naming convention:

dplyr::glimpse(quercus_lags)
#> Rows: 789
#> Columns: 34
#> $ quercus__0  <dbl> 95.5869512, 134.9473077, 135.5032469, 102.7573460, 78.5362…
#> $ quercus__1  <dbl> 134.9473077, 135.5032469, 102.7573460, 78.5362180, 144.577…
#> $ quercus__2  <dbl> 135.5032469, 102.7573460, 78.5362180, 144.5770506, 130.868…
#> $ quercus__3  <dbl> 102.7573460, 78.5362180, 144.5770506, 130.8689767, 107.072…
#> $ quercus__4  <dbl> 78.5362180, 144.5770506, 130.8689767, 107.0723299, 84.5673…
#> $ quercus__5  <dbl> 144.5770506, 130.8689767, 107.0723299, 84.5673993, 59.7365…
#> $ quercus__6  <dbl> 130.8689767, 107.0723299, 84.5673993, 59.7365964, 82.09479…
#> $ quercus__7  <dbl> 107.0723299, 84.5673993, 59.7365964, 82.0947989, 37.212402…
#> $ quercus__8  <dbl> 84.5673993, 59.7365964, 82.0947989, 37.2124029, 0.0000000,…
#> $ quercus__9  <dbl> 59.7365964, 82.0947989, 37.2124029, 0.0000000, 0.0000000, …
#> $ quercus__10 <dbl> 82.0947989, 37.2124029, 0.0000000, 0.0000000, 1.0420467, 0…
#> $ rain__0     <dbl> 1.570000, 1.569424, 1.561583, 1.551496, 1.540789, 1.532796…
#> $ rain__1     <dbl> 1.569424, 1.561583, 1.551496, 1.540789, 1.532796, 1.525082…
#> $ rain__2     <dbl> 1.561583, 1.551496, 1.540789, 1.532796, 1.525082, 1.521579…
#> $ rain__3     <dbl> 1.551496, 1.540789, 1.532796, 1.525082, 1.521579, 1.524918…
#> $ rain__4     <dbl> 1.540789, 1.532796, 1.525082, 1.521579, 1.524918, 1.524046…
#> $ rain__5     <dbl> 1.532796, 1.525082, 1.521579, 1.524918, 1.524046, 1.509918…
#> $ rain__6     <dbl> 1.525082, 1.521579, 1.524918, 1.524046, 1.509918, 1.490164…
#> $ rain__7     <dbl> 1.521579, 1.524918, 1.524046, 1.509918, 1.490164, 1.479539…
#> $ rain__8     <dbl> 1.524918, 1.524046, 1.509918, 1.490164, 1.479539, 1.485871…
#> $ rain__9     <dbl> 1.524046, 1.509918, 1.490164, 1.479539, 1.485871, 1.503371…
#> $ rain__10    <dbl> 1.509918, 1.490164, 1.479539, 1.485871, 1.503371, 1.504261…
#> $ temp__0     <dbl> 14.082412, 14.003592, 13.963610, 13.962222, 13.994756, 14.…
#> $ temp__1     <dbl> 14.003592, 13.963610, 13.962222, 13.994756, 14.074843, 14.…
#> $ temp__2     <dbl> 13.963610, 13.962222, 13.994756, 14.074843, 14.159573, 14.…
#> $ temp__3     <dbl> 13.962222, 13.994756, 14.074843, 14.159573, 14.214738, 14.…
#> $ temp__4     <dbl> 13.994756, 14.074843, 14.159573, 14.214738, 14.203480, 14.…
#> $ temp__5     <dbl> 14.074843, 14.159573, 14.214738, 14.203480, 14.072493, 13.…
#> $ temp__6     <dbl> 14.159573, 14.214738, 14.203480, 14.072493, 13.798291, 13.…
#> $ temp__7     <dbl> 14.214738, 14.203480, 14.072493, 13.798291, 13.514943, 13.…
#> $ temp__8     <dbl> 14.203480, 14.072493, 13.798291, 13.514943, 13.153375, 12.…
#> $ temp__9     <dbl> 14.072493, 13.798291, 13.514943, 13.153375, 12.558464, 11.…
#> $ temp__10    <dbl> 13.798291, 13.514943, 13.153375, 12.558464, 11.686879, 10.…
#> $ time        <dbl> 0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.5, 10.5, 11…
quercus_lags |> 
  dplyr::select(
    quercus__0,
    quercus__5,
    quercus__10,
    time
  ) |> 
  dplyr::filter(
    time <= 100
  ) |>
  distantia::tsl_init(
    time_column = "time"
  ) |> 
  distantia::tsl_plot()

Ecological Memory Analysis

The computeMemory() function fits Random Forest models on the lagged data. It measures variable importance using permutation, which is robust to multicollinearity and temporal autocorrelation.

Two benchmark modes are available for significance testing:

  • "white.noise": Random values without temporal structure (faster)
  • "autocorrelated": Random walk with temporal structure (more conservative, recommended)

The model runs multiple times (repetitions), regenerating the random term each time, then computes percentiles of importance scores.

quercus_memory <- memoria::computeMemory(
  lagged.data = quercus_lags,
  random.mode = "autocorrelated",
  repetitions = 100
)

We can visualize the results with plotMemory().

memoria::plotMemory(quercus_memory)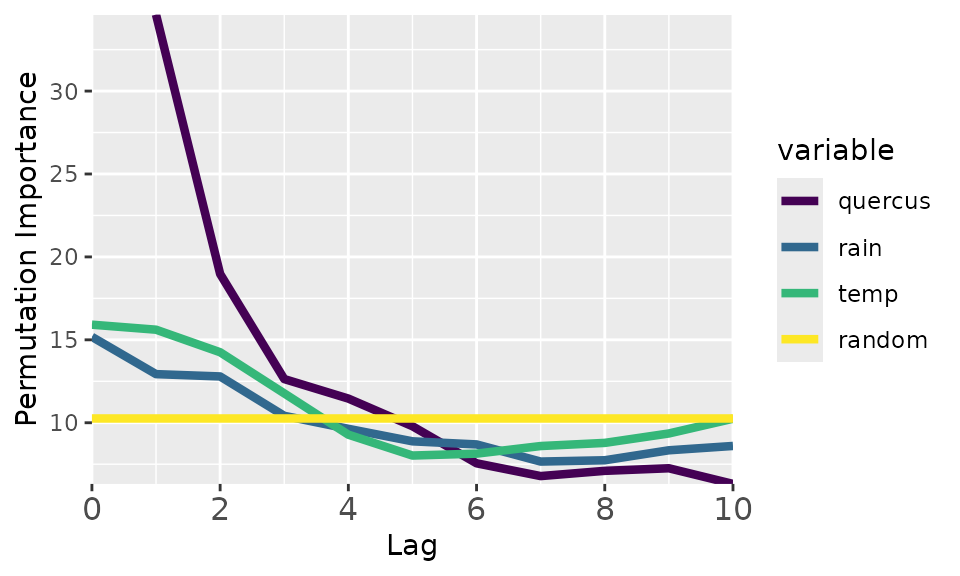

The plot shows all ecological memory components of this dataset.

  • Endogenous memory (“quercus” curve): shows the importance of the past pollen abundance in predicting current pollen abundance. In this case, this is the most important memory component, with a lag of ~5000 years.

  • Significance test (“random” curve): shows the median importance scores of randomly generated variables. Defines a baseline helpful to know when a given memory component explains the response better (above the yellow line) or worse than random.

  • Concurrent effect (“temp” and “rain” at lag 0): importance of the current driver values to predict the response. In this case, the concurrent effect is much weaker than the endogenous memory.

  • Exogenous memory (“temp” and “rain” at lag > 0): importance of the past driver values in explaining the current response values. According to the plot, temperature is the strongest component of the exogenous memory, with a lag of almost ~4000 years.

The extractMemoryFeatures() function transforms the plot results into quantitative features:

extractMemoryFeatures(
  memory.pattern = quercus_memory
) |> 
  dplyr::glimpse()
#> Rows: 1
#> Columns: 8
#> $ label                <chr> "quercus"
#> $ strength.endogenous  <dbl> 24.35066
#> $ strength.exogenous   <dbl> 5.351078
#> $ strength.concurrent  <dbl> 5.653404
#> $ length.endogenous    <dbl> 0.4
#> $ length.exogenous     <dbl> 0.3
#> $ dominance.endogenous <dbl> 0.4
#> $ dominance.exogenous  <dbl> 0

The output contains eight features organized in three groups:

The strength values (scaled to [0, 1] by default) measure the peak importance of each memory component relative to the median of the random baseline.

The length values (proportion in [0, 1]) measure how far into the past each memory component remains above the random baseline. In this case, the endogenous memory component is above the baseline for half of the lags.

The dominance values (proportion in [0, 1]) measure whether endogenous or exogenous memory prevails across significant lags. In this case, the exogenous memory is never above the endogenous one, hence it has zero dominance.

Summary

The complete workflow:

  1. alignTimeSeries() - Align datasets with different resolutions.
  2. lagTimeSeries() - Create lag structure.
  3. computeMemory() - Fit Random Forest and compute importance.
  4. plotMemory() - Visualize the memory pattern.
  5. extractMemoryFeatures() - Quantify memory characteristics.