Plots a Moran's I test of model residuals

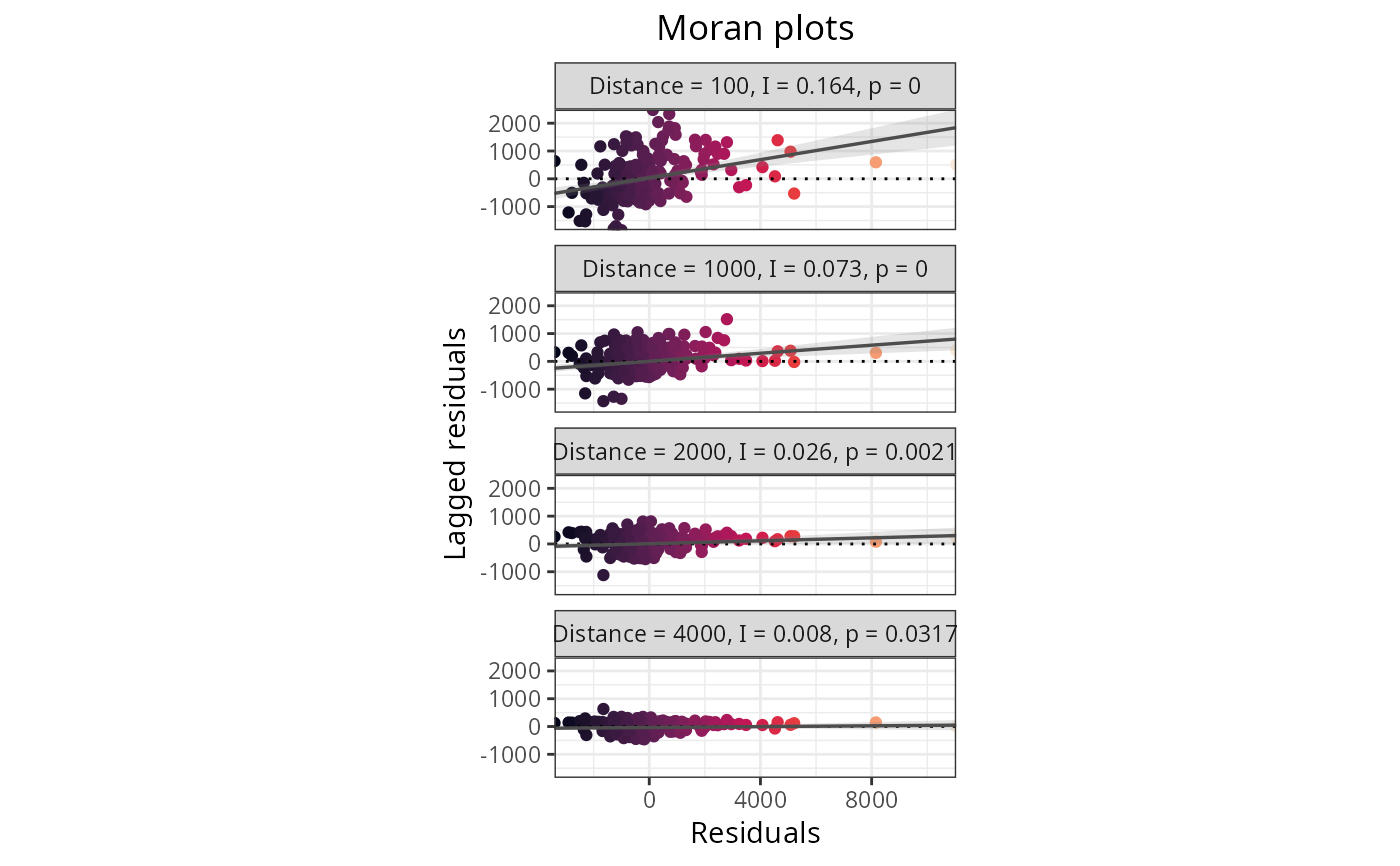
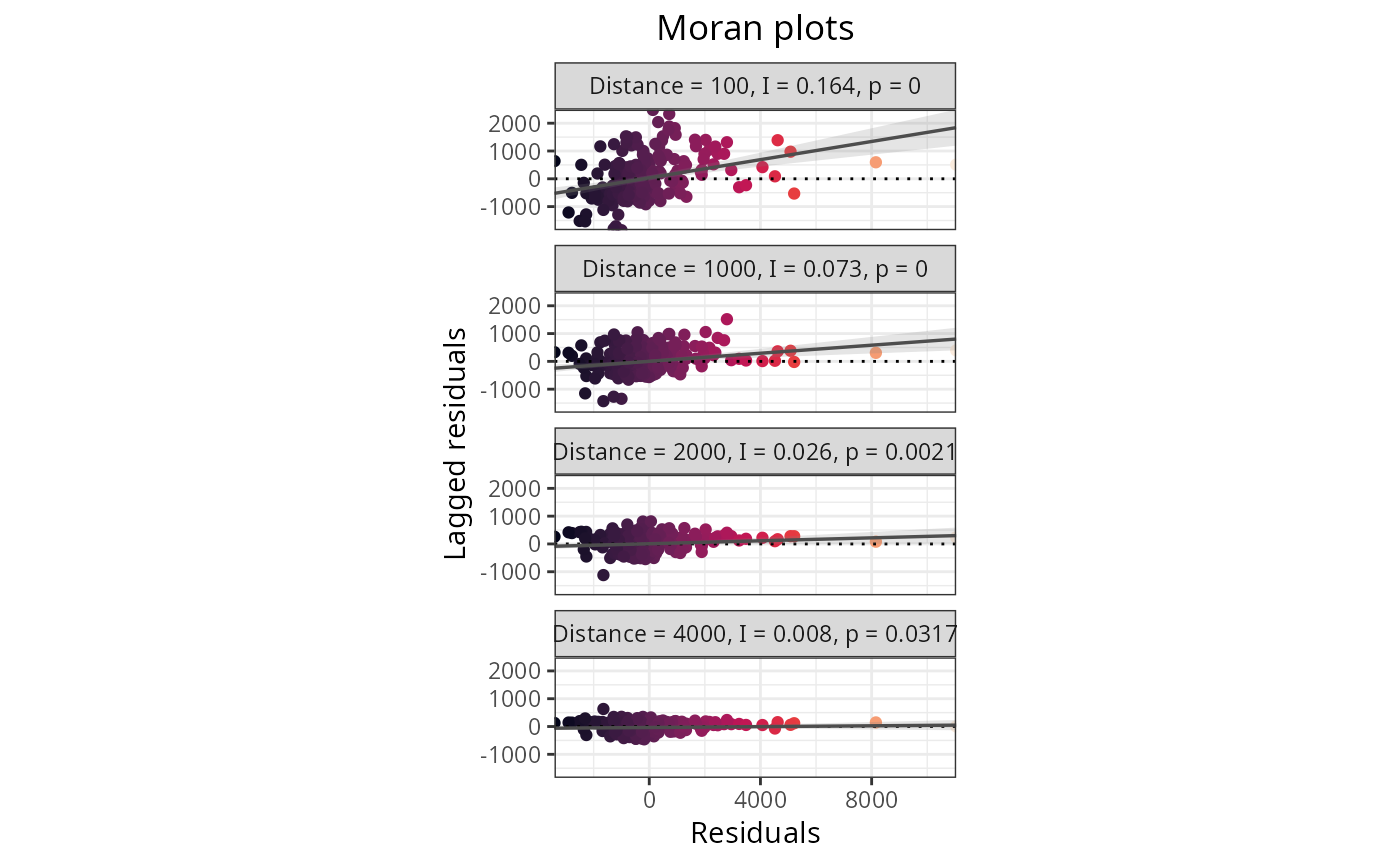
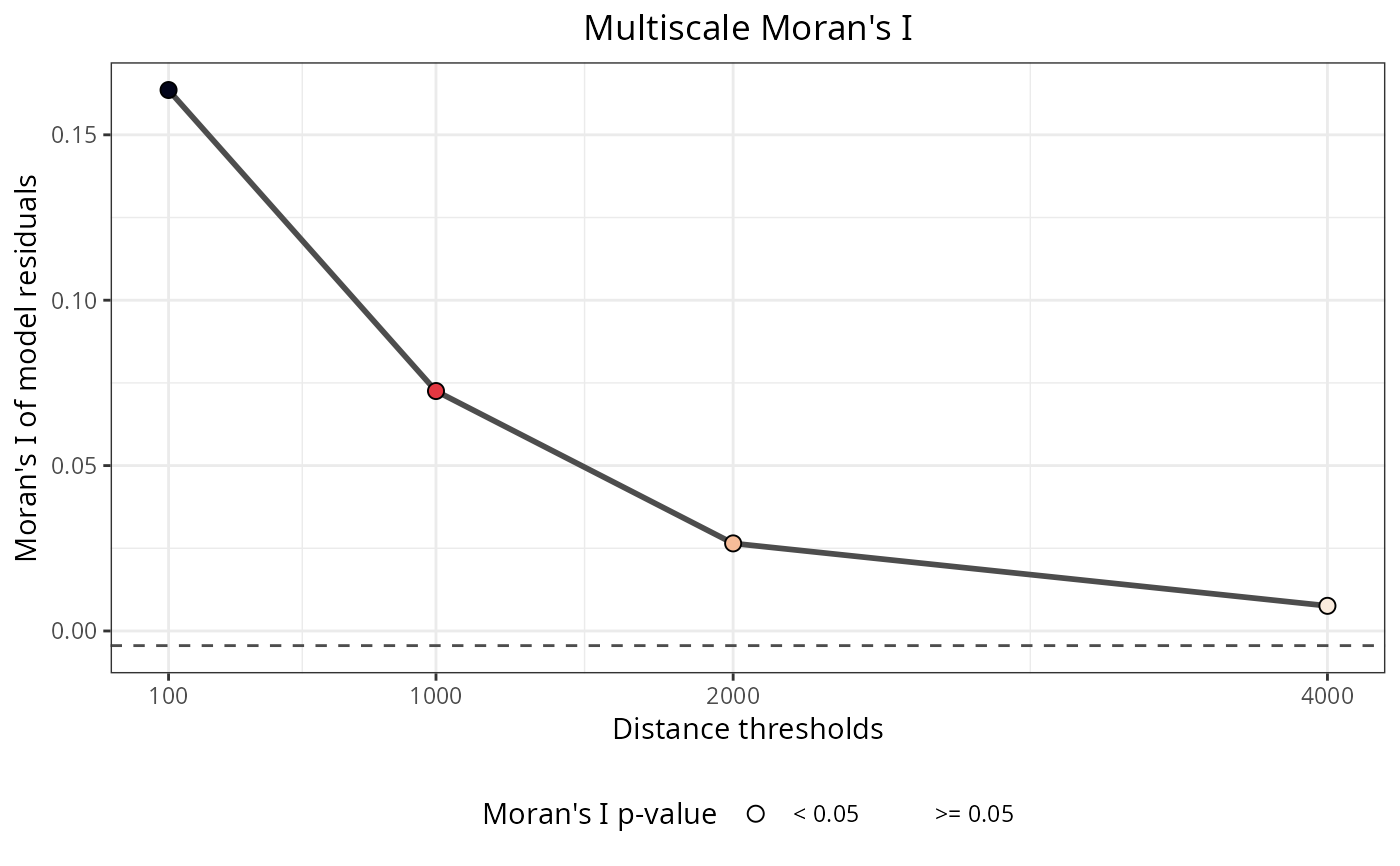
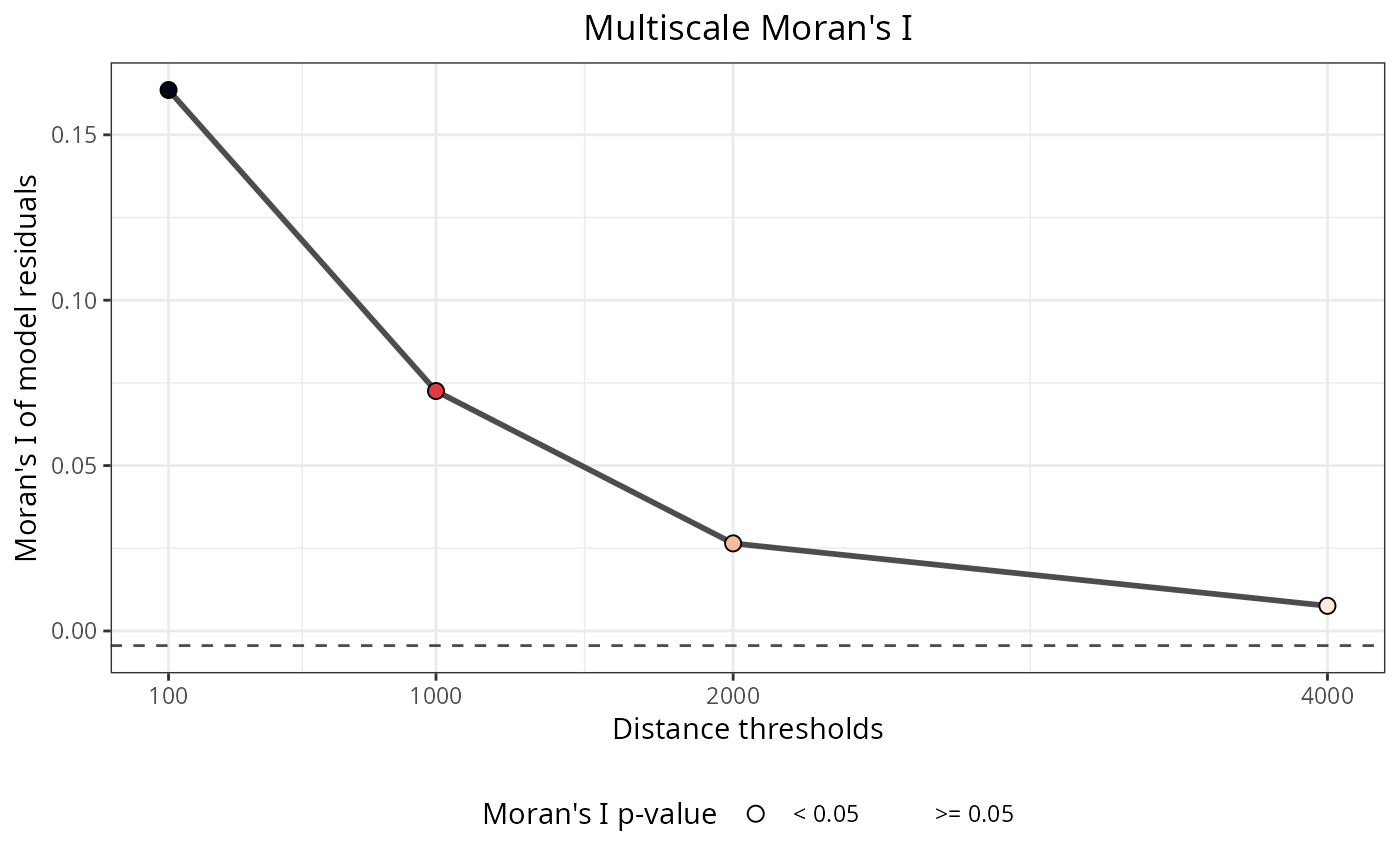
Plots the results of spatial autocorrelation tests for a variety of functions within the package. The x axis represents the Moran's I estimate, the y axis contains the values of the distance thresholds, the dot sizes represent the p-values of the Moran's I estimate, and the red dashed line represents the theoretical null value of the Moran's I estimate.

Usage

plot_moran(
  model,
  point.color = viridis::viridis(
    100,
    option = "F",
    direction = -1
   ),
  line.color = "gray30",
  option = 1,
  ncol = 1,
  verbose = TRUE
)

Arguments

model

A model fitted with rf(), rf_repeat(), or rf_spatial(), or a data frame generated by moran(). Default: NULL

point.color

Colors of the plotted points. Can be a single color name (e.g. "red4"), a character vector with hexadecimal codes (e.g. "#440154FF" "#21908CFF" "#FDE725FF"), or function generating a palette (e.g. viridis::viridis(100)). Default: viridis::viridis(100, option = "F")

line.color

Character string, color of the line produced by ggplot2::geom_smooth(). Default: "gray30"

option

Integer, type of plot. If 1 (default) a line plot with Moran's I and p-values across distance thresholds is returned. If 2, scatterplots of residuals versus lagged residuals per distance threshold and their corresponding slopes are returned. In models fitted with rf_repeat(), the residuals and lags of the residuals are computed from the median residuals across repetitions. Option 2 is disabled if x is a data frame generated by moran().

ncol

Number of columns of the plot. Only relevant when option = 2. Argument ncol of wrap_plots.

verbose

Logical, if TRUE, the resulting plot is printed, Default: TRUE

Value

A ggplot.

See also

moran(), moran_multithreshold()

Other visualization: plot_evaluation(), plot_importance(), plot_optimization(), plot_residuals_diagnostics(), plot_response_curves(), plot_response_surface(), plot_training_df(), plot_training_df_moran(), plot_tuning()

Examples

data(plants_rf)

plot_moran(plants_rf)



plot_moran(plants_rf, option = 2)