Mapping Time Series Dissimilarity

Summary

This article showcases different spatial representations of the outputs of distantia() and momentum().

Setup

library(distantia, warn.conflicts = FALSE)
library(dplyr, warn.conflicts = FALSE)
library(mapview, warn.conflicts = FALSE)

Mapping Results of distantia() Functions

The functions with the prefix distantia quantify time series dissimilarity and provide results that can be represented as maps.

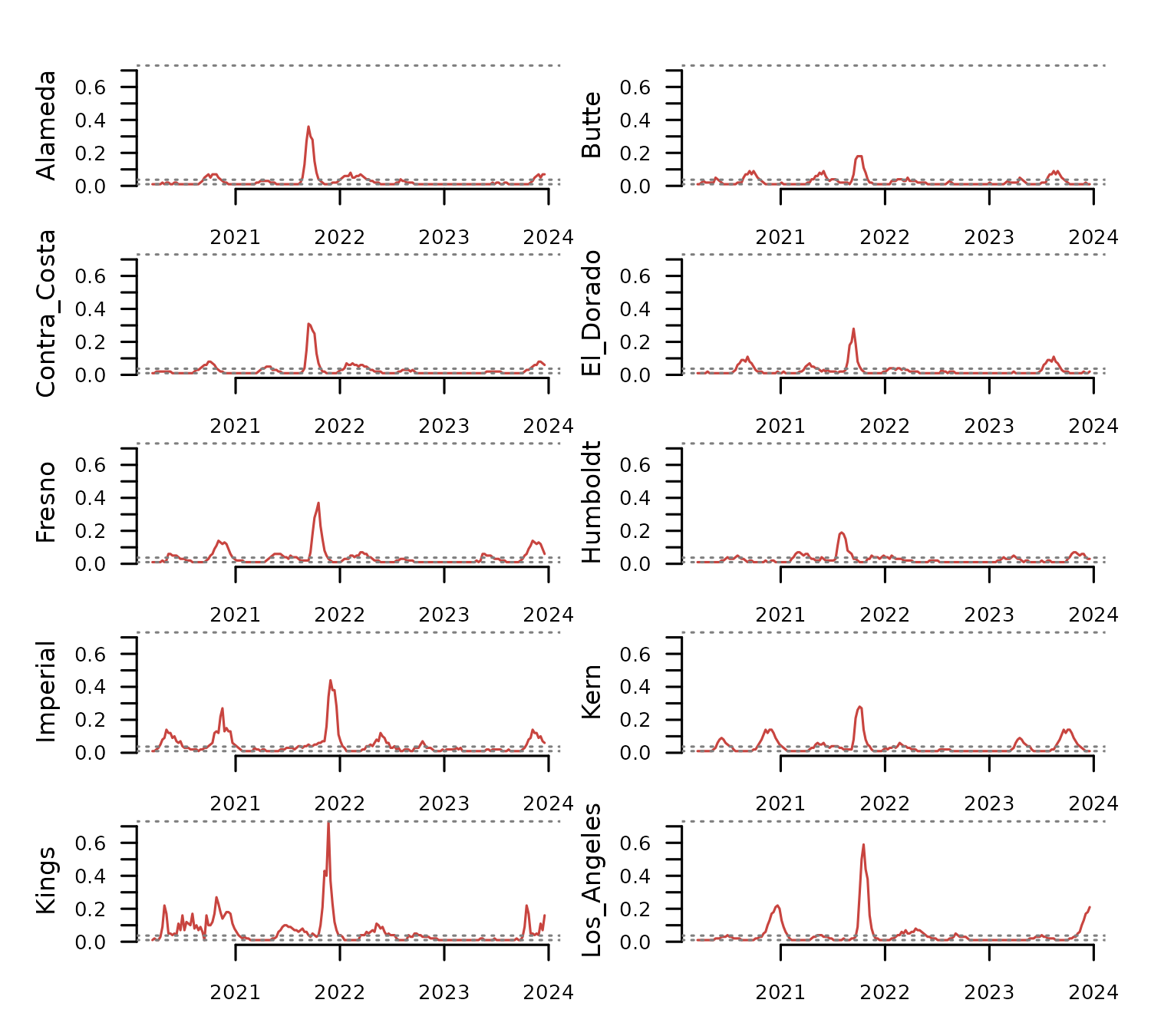
Example Data

The examples in this article illustrate how to map dissimilarity scores using the datasets covid_prevalence and covid_polygons included with distantia. The dataset comprises time series of weekly Covid-19 prevalence in several California counties.

tsl <- distantia::tsl_initialize(
  x = distantia::covid_prevalence,
  name_column = "name",
  time_column = "time"
)

distantia::tsl_plot(
  tsl = tsl[1:10],
  columns = 2,
  guide = FALSE
)

The map below displays the polygons in distantia::covid_counties using mapview().

mapview::mapview(
  distantia::covid_counties,
  label = "name"
)

Dissimilarity Analysis

The code in this section prepares several datasets to use in the different mapping examples:

• df_psi: a lock-step dissimilarity data frame with psi scores and p-values from restricted permutation tests.
• df_stats: dissimilarity stats of each time series against all others.
• df_cluster: a hierarchical clustering based on the dissimilarity scores in df_psi.

The lock-step dissimilarity analysis shown below includes p-values from a restricted permutation test. These p-values will be useful as criteria to select relevant mapping features.

#parallelization setup
future::plan(
  future::multisession,
  workers = parallelly::availableCores() - 1
  )

#lock-step dissimilarity analysis
df_psi <- distantia::distantia(
  tsl = tsl,
  distance = "euclidean",
  lock_step = TRUE,
  repetitions = 1000,
  permutation = "restricted",
  block_size = 12 #weeks
)

#disable parallelization
future::plan(
  future::sequential
  )

#check resulting data frame
df_psi |> 
  dplyr::select(x, y, psi, p_value) |> 
  dplyr::glimpse()
#> Rows: 630
#> Columns: 4
#> $ x       <chr> "Napa", "Alameda", "Alameda", "Sacramento", "San_Joaquin", "Sa…
#> $ y       <chr> "Solano", "San_Mateo", "Contra_Costa", "Sonoma", "Stanislaus",…
#> $ psi     <dbl> 0.8726115, 1.0656371, 1.1620553, 1.2578125, 1.2919255, 1.29793…
#> $ p_value <dbl> 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001, 0.001,…

The code below aggregates psi scores in the data frame df_psi to summarize the overall dissimilarity of each time series with all others.

df_stats <- distantia::distantia_stats(
  df = df_psi
)

df_stats |> 
  dplyr::select(
    name, mean
  ) |> 
  dplyr::glimpse()
#> Rows: 36
#> Columns: 2
#> $ name <chr> "Alameda", "Butte", "Contra_Costa", "El_Dorado", "Fresno", "Humbo…
#> $ mean <dbl> 3.214531, 3.266749, 3.358524, 3.546757, 3.270684, 4.028824, 3.834…

The function distantia_cluster_hclust() runs a hierarchical clustering using the psi scores in df_psi as clustering criteria.

df_cluster <- distantia::distantia_cluster_hclust(
  df = df_psi
)$df

df_cluster |> 
  dplyr::select(name, cluster) |>
  dplyr::glimpse()
#> Rows: 36
#> Columns: 2
#> $ name    <chr> "Napa", "Alameda", "Sacramento", "San_Joaquin", "Santa_Clara",…
#> $ cluster <dbl> 1, 2, 2, 1, 3, 2, 2, 3, 2, 1, 1, 1, 2, 1, 2, 4, 2, 1, 1, 1, 2,…

Network Map

The function distantia_spatial() transforms the result of distantia() to an sf data frame with edges connecting time series coordinates or polygons. The result can be interpreted as a dissimilarity network.

sf_network <- distantia::distantia_spatial(
  df = df_psi,
  sf = distantia::covid_counties |> 
    dplyr::select(
      name, geometry
    ),
  network = TRUE
)

dplyr::glimpse(sf_network)
#> Rows: 630
#> Columns: 9
#> $ edge_name <chr> "Alameda - Butte", "Alameda - Contra_Costa", "Butte - Contra…
#> $ y         <chr> "Butte", "Contra_Costa", "Contra_Costa", "El_Dorado", "El_Do…
#> $ x         <chr> "Alameda", "Alameda", "Butte", "Butte", "Contra_Costa", "Ala…
#> $ psi       <dbl> 2.962963, 1.162055, 2.733068, 2.327273, 2.767442, 2.483755, …
#> $ p_value   <dbl> 0.038, 0.001, 0.001, 0.004, 0.015, 0.002, 0.079, 1.000, 0.33…
#> $ null_mean <dbl> 3.253452, 2.442545, 3.453084, 2.857149, 3.273194, 3.050181, …
#> $ null_sd   <dbl> 0.16577079, 0.27674638, 0.20054408, 0.19082565, 0.22631966, …
#> $ geometry  <LINESTRING [°]> LINESTRING (-121.8869 37.64..., LINESTRING (-121.…
#> $ length    <dbl> 226007.5, 30278.1, 196579.9, 135288.6, 155203.7, 173206.4, 2…

The resulting sf data frame has a field with the edge name, the columns x and y with the names of the connected time series, the psi scores and p-values of the dissimilarity data frame, a geometry column of type LINESTRING defining the network edges, and the length of the edges.

This sf data frame can be mapped right away, but in this case there are too many pairs of counties to achieve a meaningful map.

mapview::mapview(
  sf_network,
  layer.name = "Psi",
  label = "edge_name",
  zcol = "psi",
  color = distantia::color_continuous()
)

Focusing on particular aspects of the data at hand may help untangle this mess. For example, the code below subsets edges connecting with San Francisco and its most similar counties in terms of Covid19 prevalence.

#select pairs of counties
counties <- c(
  "Los_Angeles", 
  "San_Francisco", 
  "Fresno", 
  "San_Joaquin",
  "Monterey"
  )

sf_network_subset <- sf_network[
  which(
    sf_network$x %in% counties & 
      sf_network$y %in% counties
    ), 
  ]

#map country polygons and dissimilarity edges
mapview::mapview(
  covid_counties,
  col.regions = NA,
  alpha.regions = 0,
  color = "black",
  label = "name",
  legend = FALSE,
  map.type = "OpenStreetMap"
) +
  mapview::mapview(
    sf_network_subset,
    layer.name = "Psi",
    label = "edge_name",
    zcol = "psi",
    lwd = 5,
    color = distantia::color_continuous(
      rev = TRUE
      )
  )

The function distantia_spatial() also has a one-to-many mode designed to help map the dissimilarity of one time series against all others.

sf_network <- distantia::distantia_spatial(
  df = df_psi,
  sf = distantia::covid_counties |> 
    dplyr::select(
      name, geometry
    ),
  network = FALSE
)

dplyr::glimpse(sf_network)
#> Rows: 1,295
#> Columns: 7
#> $ x         <chr> "Alameda", "Alameda", "Alameda", "Alameda", "Alameda", "Alam…
#> $ y         <chr> "Alameda", "Butte", "Contra_Costa", "El_Dorado", "Fresno", "…
#> $ psi       <dbl> 0.000000, 2.962963, 1.162055, 2.483755, 3.456869, 3.960000, …
#> $ p_value   <dbl> 0.000, 0.038, 0.001, 0.002, 0.334, 0.979, 0.208, 0.109, 0.98…
#> $ null_mean <dbl> 0.000000, 3.253452, 2.442545, 3.050181, 3.565789, 3.638864, …
#> $ null_sd   <dbl> 0.00000000, 0.16577079, 0.27674638, 0.20253761, 0.23818318, …
#> $ geometry  <MULTIPOLYGON [°]> MULTIPOLYGON (((-121.9907 3..., MULTIPOLYGON ((…

This option does not create edges, and instead uses the geometry introduced in the sf argument. This sf data frame is mapped as follows: when one site in the “x” column is selected, the result shows the dissimilarity scores of all other sites against the selected one.

#subset one county
sf_network_subset <- sf_network[
  sf_network$x == "San_Francisco", 
  ]

#one-to-many visualization
mapview::mapview(
    sf_network_subset,
    layer.name = "Psi",
    label = "y",
    zcol = "psi",
    col.regions = distantia::color_continuous(
      rev = TRUE
      )
  )

Dissimilarity Stats Map

Mapping the dissimilarity stats of each time series may help identify places that are somewhat special because they show a high dissimilarity with all others, or places that are average and have no distinctive features.

Merging the dissimilarity stats with the sf data frame containing the county polygons generates the spatial data required for the map.

sf_stats <- merge(
  x = distantia::covid_counties,
  y = df_stats
) |> 
  dplyr::select(
    mean,
    name
  )

The map below uses warm colors to highlight places with a high dissimilarity with all others, such as Humboldt county in the north west of the state.

mapview::mapview(
  sf_stats,
  layer.name = "Psi mean",
  zcol = "mean",
  label = "name",
  col.regions = distantia::color_continuous(
    rev = TRUE
  ),
  alpha.regions = 1
)

Clustering Map

This section shows how to map the similarity groups resulting from distantia::distantia_cluster_hclust() or distantia::distantia_cluster_kmeans().

The first block in the code below joins the county polygons in distantia::covid_polygons with the clustering data frame df_cluster. This block also generates the variable “alpha” from the column “silhouette_width”, which represents the strength of membership to the assigned clustering group.

The second block generates the map, using colors for cluster membership, and the variable alpha to code the strenght of membership. This setup allows identifying groups of similar counties while highlighting counties that somehow do not fully belong to their given group. This is the case of Butte, which is in the group 5, but with a very low silhouette score.

#join county polygons with clustering groups
sf_cluster <- distantia::covid_counties |> 
  dplyr::select(name, geometry) |> 
  dplyr::inner_join(
    y = df_cluster,
    by = "name"
  ) |> 
  #remap silhouette score to transparency values
  dplyr::mutate(
    alpha = f_rescale_local(
      x = silhouette_width,
      new_min = 0.1
      )
  )

mapview::mapview(
  sf_cluster,
  layer.name = "Group",
  zcol = "cluster",
  label = "name",
  col.regions = distantia::color_continuous(
    n = max(sf_cluster$cluster)
  ),
  alpha.regions = sf_cluster$alpha
)

Mapping Results of momentum()

The momentum functions quantify the contribution to dissimilarity of individual variables in multivariate time series. The results of momentum functions are slightly harder to map due to a high cardinality (number of time series times number of variables), but distantia provides some tools to face this challenge.

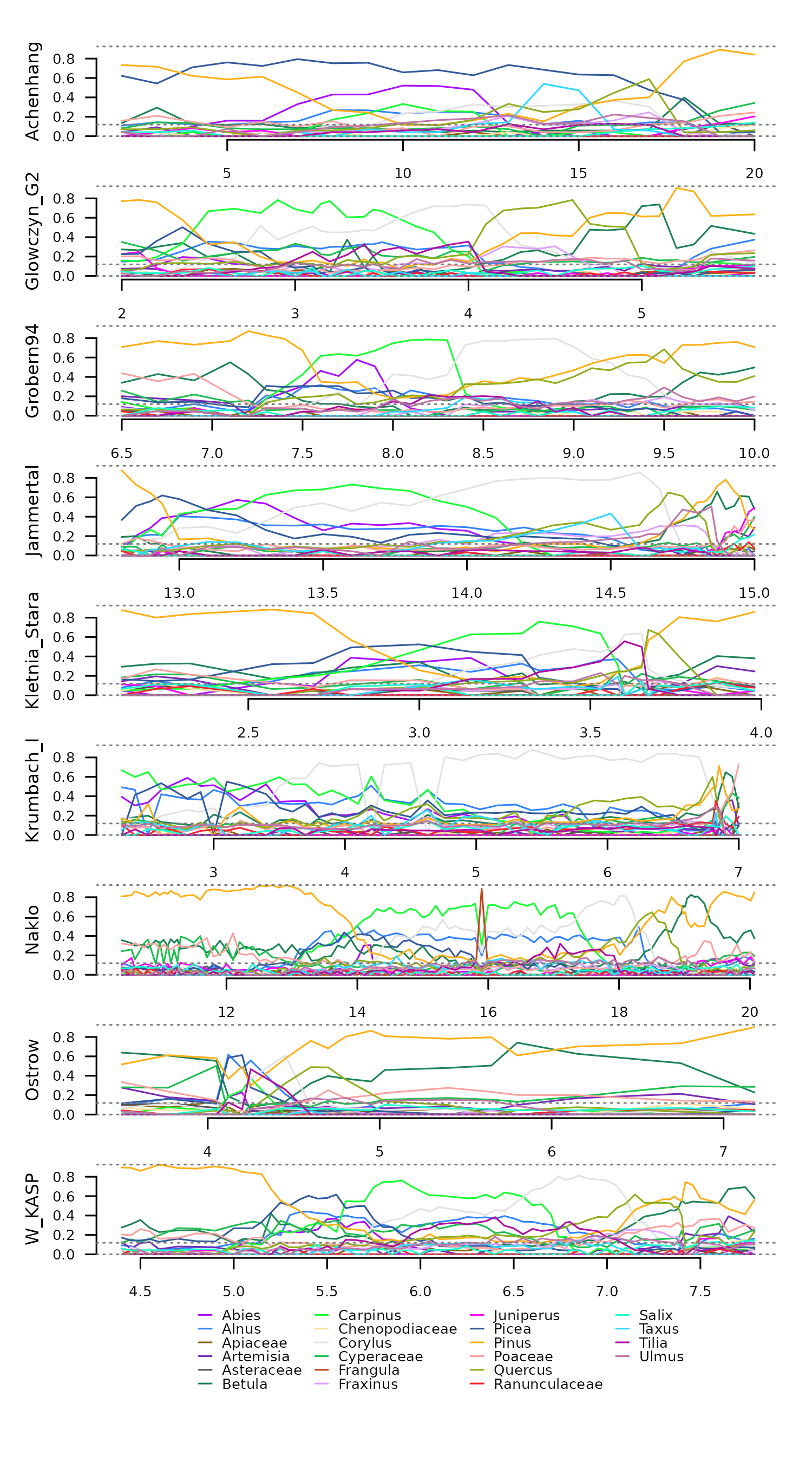
Example Data

This example uses the data eemian_pollen and eemian_coordinates, which comprises nine irregular time series of pollen counts in Central Uurope from the Last Interglacial (Eemian period). This data requires a Hellinger transformation to facilitate dissimilarity analyses.

tsl <- distantia::tsl_initialize(
  x = distantia::eemian_pollen,
  name_column = "name",
  time_column = "time"
) |> 
  distantia::tsl_transform(
    f = distantia::f_hellinger
  )
#> distantia::utils_prepare_time():  duplicated time indices in 'Krumbach_I':
#> - value 6.8 replaced with 6.825.

distantia::tsl_plot(
  tsl = tsl,
  guide_columns = 4
)

Importance Analysis

The function momentum_dtw() computes variable importance using a jackknife approach. The column “importance” represents contribution to similarity and dissimilarity with negative and positive values, respectively.

df_importance <- momentum_dtw(
  tsl = tsl
)

head(df_importance, n = 20)
#>            x           y      psi       variable importance
#> 1  Achenhang Glowczyn_G2 3.838195          Pinus -43.665268
#> 2  Achenhang Glowczyn_G2 3.838195        Corylus  14.120167
#> 3  Achenhang Glowczyn_G2 3.838195       Carpinus  54.101955
#> 4  Achenhang Glowczyn_G2 3.838195         Betula -46.158001
#> 5  Achenhang Glowczyn_G2 3.838195        Quercus -59.247194
#> 6  Achenhang Glowczyn_G2 3.838195          Alnus  -2.616569
#> 7  Achenhang Glowczyn_G2 3.838195          Picea 252.368040
#> 8  Achenhang Glowczyn_G2 3.838195        Poaceae -51.436966
#> 9  Achenhang Glowczyn_G2 3.838195     Cyperaceae   8.966638
#> 10 Achenhang Glowczyn_G2 3.838195          Abies  50.463741
#> 11 Achenhang Glowczyn_G2 3.838195          Ulmus -48.178867
#> 12 Achenhang Glowczyn_G2 3.838195          Tilia   8.382970
#> 13 Achenhang Glowczyn_G2 3.838195       Frangula   0.000000
#> 14 Achenhang Glowczyn_G2 3.838195      Artemisia -44.046944
#> 15 Achenhang Glowczyn_G2 3.838195       Fraxinus -51.581281
#> 16 Achenhang Glowczyn_G2 3.838195          Taxus -33.468362
#> 17 Achenhang Glowczyn_G2 3.838195      Juniperus -40.434843
#> 18 Achenhang Glowczyn_G2 3.838195 Chenopodiaceae -65.650250
#> 19 Achenhang Glowczyn_G2 3.838195          Salix -64.341357
#> 20 Achenhang Glowczyn_G2 3.838195     Asteraceae -64.395450
#>                  effect
#> 1  increases similarity
#> 2  decreases similarity
#> 3  decreases similarity
#> 4  increases similarity
#> 5  increases similarity
#> 6  increases similarity
#> 7  decreases similarity
#> 8  increases similarity
#> 9  decreases similarity
#> 10 decreases similarity
#> 11 increases similarity
#> 12 decreases similarity
#> 13 increases similarity
#> 14 increases similarity
#> 15 increases similarity
#> 16 increases similarity
#> 17 increases similarity
#> 18 increases similarity
#> 19 increases similarity
#> 20 increases similarity

Network Map

The function momentum_spatial(), just like distantia_spatial(), transforms the results of momentum functions to an sf data frame with edges.

sf_network <- distantia::momentum_spatial(
  df = df_importance,
  sf = distantia::eemian_coordinates |> 
    dplyr::select(
      name, geometry
    ),
  network = TRUE
)

dplyr::glimpse(sf_network)
#> Rows: 36
#> Columns: 30
#> $ edge_name                  <chr> "Achenhang - Glowczyn_G2", "Achenhang - Gro…
#> $ y                          <chr> "Glowczyn_G2", "Grobern94", "Grobern94", "J…
#> $ x                          <chr> "Achenhang", "Achenhang", "Glowczyn_G2", "A…
#> $ psi                        <dbl> 3.838195, 3.457364, 2.150206, 3.345726, 2.4…
#> $ most_similarity            <chr> "Apiaceae", "Apiaceae", "Salix", "Chenopodi…
#> $ most_dissimilarity         <chr> "Picea", "Picea", "Cyperaceae", "Picea", "J…
#> $ importance__Abies          <dbl> 50.463741, -34.521977, 34.730386, 20.887151…
#> $ importance__Alnus          <dbl> -2.61656907, -60.17012299, 24.39570778, -23…
#> $ importance__Apiaceae       <dbl> -68.043334, -82.849382, -5.805649, -42.2206…
#> $ importance__Artemisia      <dbl> -44.046944, -18.673252, -16.037820, -45.043…
#> $ importance__Asteraceae     <dbl> -64.395450, -72.687395, -18.353833, -62.659…
#> $ importance__Betula         <dbl> -46.1580012, -19.8837735, -27.4911174, -3.2…
#> $ importance__Carpinus       <dbl> 54.101955, 9.859379, -16.944538, 41.740684,…
#> $ importance__Chenopodiaceae <dbl> -65.650250, -52.803828, -15.985173, -64.744…
#> $ importance__Corylus        <dbl> 14.1201674, 8.0338601, -23.4297701, 57.2593…
#> $ importance__Cyperaceae     <dbl> 8.966638, -40.595718, 130.316987, -63.71292…
#> $ importance__Frangula       <dbl> 0.00000, 0.00000, 0.00000, 0.00000, 0.00000…
#> $ importance__Fraxinus       <dbl> -51.5812807, -42.7763431, 23.6744565, -42.1…
#> $ importance__Juniperus      <dbl> -40.43484324, -43.34005481, 114.60113107, -…
#> $ importance__Picea          <dbl> 252.368040, 284.131985, 39.516200, 228.1667…
#> $ importance__Pinus          <dbl> -43.665268, -28.802281, -9.383143, -43.3449…
#> $ importance__Poaceae        <dbl> -51.4369663, -45.1372588, 2.1673727, -57.14…
#> $ importance__Quercus        <dbl> -59.2471936, -41.9994999, 25.2057451, -46.7…
#> $ importance__Ranunculaceae  <dbl> -57.51235321, -65.41178095, -33.45096902, -…
#> $ importance__Salix          <dbl> -64.34136, -63.56730, -42.41996, -48.75841,…
#> $ importance__Taxus          <dbl> -33.468362, -45.334284, 35.555829, -42.8579…
#> $ importance__Tilia          <dbl> 8.3829701, -20.9450048, -32.2572297, -41.57…
#> $ importance__Ulmus          <dbl> -48.178867, -50.202556, -31.838671, -28.894…
#> $ geometry                   <LINESTRING [°]> LINESTRING (12.19381 47.753..., …
#> $ length                     <dbl> 771512.45, 437377.26, 536559.23, 187660.13,…

Notice that it separates the importance of each variable to a separate column, and also has two character columns named “most_similarity” and “most_dissimilarity” with the names of the variables with the highest and lowest importance scores.

The map below shows the pairs of most similar time series connected with edges coded after the name of the variable that contributes the most to their similarity.

mapview::mapview(
  distantia::eemian_coordinates,
  layer.name = "Eemian sites - m.a.s.l",
  label = "name",
  zcol = "elevation",
  col.regions = distantia::color_continuous()
) +
mapview::mapview(
  sf_network |> 
    dplyr::filter(
      psi < mean(psi)
    ),
  layer.name = "Contributes to Similarity",
  label = "most_similarity",
  zcol = "most_similarity",
  color = distantia::color_discrete(
    n = length(unique(sf_network$most_similarity))
  )
)

Filtering the input even further allows to focus on specific features of the dataset at hand. For example, the map below highlights pairs of time series with high similarity driven mostly by the taxa “Frangula”.

mapview::mapview(
  distantia::eemian_coordinates,
  layer.name = "Eemian sites - m.a.s.l",
  label = "name",
  zcol = "elevation",
  col.regions = distantia::color_continuous()
) +
mapview::mapview(
  sf_network |> 
    dplyr::filter(
      psi < mean(psi),
      most_similarity == "Frangula"
    ),
  layer.name = "Contributes to Similarity",
  label = "most_similarity",
  zcol = "most_similarity",
  color = distantia::color_discrete(
    n = 1
  )
)

Conversely, we can also map what variable makes these sites more different.

mapview::mapview(
  distantia::eemian_coordinates,
  layer.name = "Eemian sites - m.a.s.l",
  label = "name",
  zcol = "elevation",
  col.regions = distantia::color_continuous()
) +
mapview::mapview(
  sf_network |> 
    dplyr::filter(
      psi < mean(psi),
      most_similarity == "Frangula"
    ),
  layer.name = "Contributes to Dissimilarity",
  label = "most_dissimilarity",
  zcol = "most_dissimilarity",
  color = distantia::color_discrete(
    n = length(unique(sf_network$most_dissimilarity))
  )
)