Non-Spatial Random Forest Models

Introduction

This tutorial demonstrates how to fit and interpret non-spatial random forest models using the spatialRF package. You’ll learn how to explore spatial data, find promising variable interactions, train models, evaluate performance, and understand variable importance.

If you’re interested in addressing spatial autocorrelation in your model residuals, see the Spatial Random Forest Models tutorial.

Setup

The following libraries are required for this tutorial.

library(spatialRF)
library(ggplot2)
library(dplyr)
library(DT)
library(rnaturalearth)
library(rnaturalearthdata)
library(randomForestExplainer)
library(parallel)
library(patchwork)

Many functions in the package also support a parallelization backend to speed-up execution.

cluster <- parallel::makeCluster(
  parallel::detectCores() - 1,
  type = "PSOCK"
)

The package includes the example dataset plants_df with plant species richness and predictors for 227 ecoregions in the Americas. The object plants_distance is a matrix of geographical distances between ecoregions.

data(
  plants_df,         #training data frame
  plants_response,   #response name
  plants_predictors, #predictors names
  plants_distance,   #distance matrix in km
  plants_xy          #case coordinates of plants_df
  )

#distance thresholds (same units as plants_distance, km)
#used to assess spatial correlation at different distances
distance_thresholds <- c(10, 100, 1000, 2000, 4000, 8000)

#a pretty color palette
colors <- grDevices::hcl.colors(
    n = 100,
    palette = "Zissou 1"
    )

The figure below shows the response variable richness_species_vascular in space.

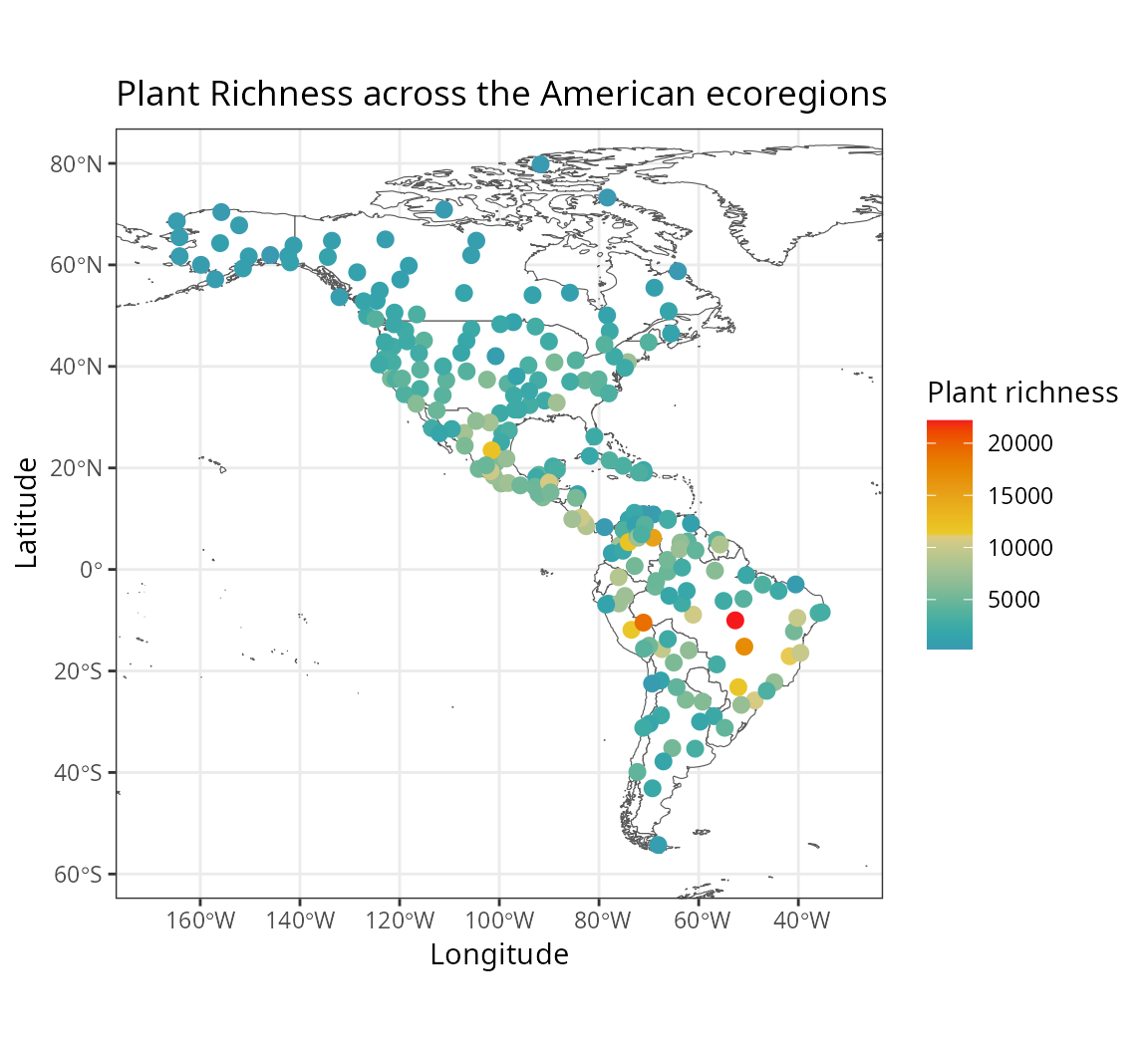
The predictors, stored in plants_predictors represent diverse factors that may influence plant richness such as sampling bias, the area of the ecoregion, climatic variables, human presence and impact, topography, geographical fragmentation, and features of the neighbors of each ecoregion.

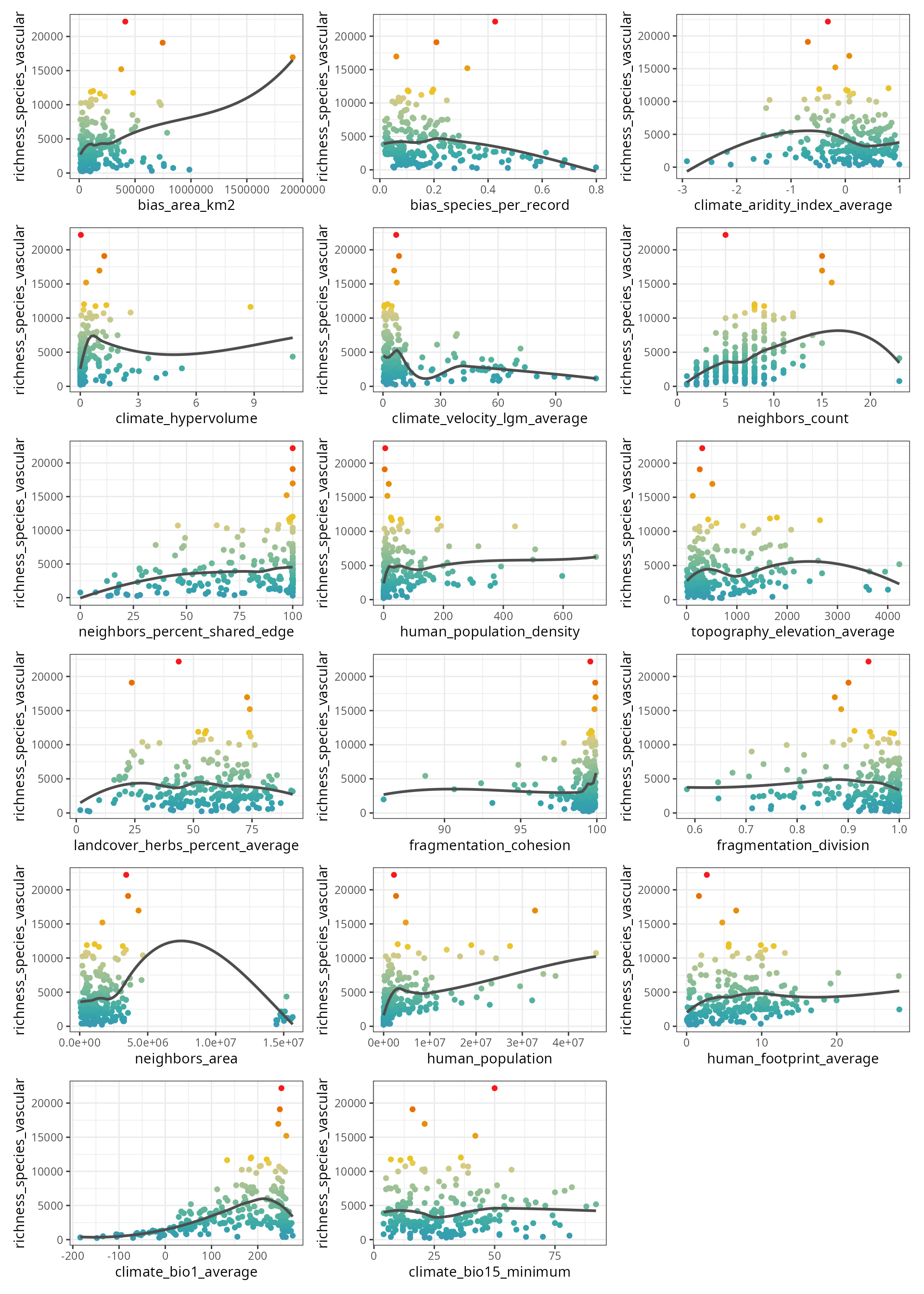
The figure below shows the scatterplots of the response variable (y axis) against each predictor (x axis).

spatialRF::plot_training_df(
  data = plants_df,
  dependent.variable.name = plants_response,
  predictor.variable.names = plants_predictors,
  point.color = colors,
  ncol = 3
  )

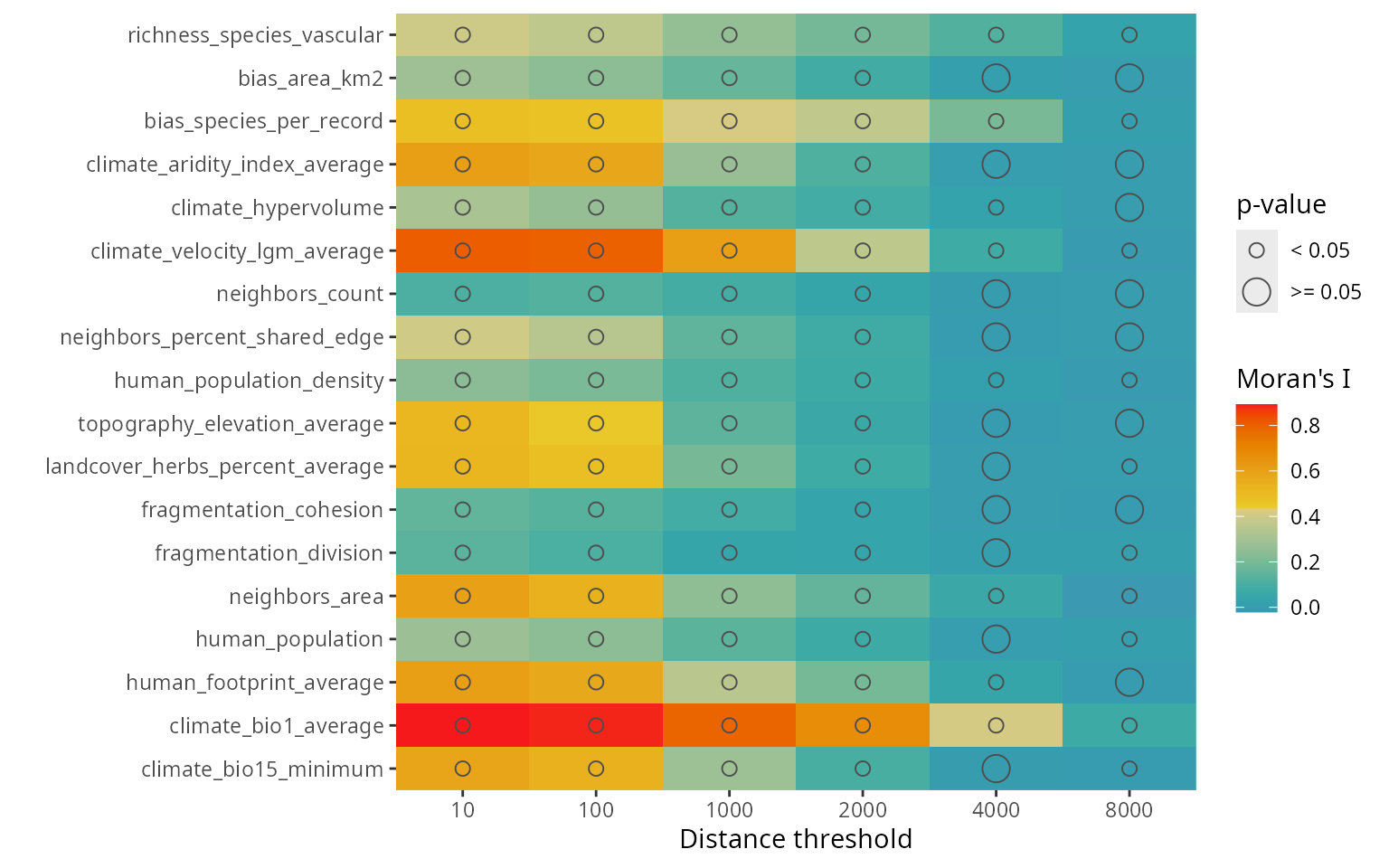
The function plot_training_df_moran() shows the spatial autocorrelation of the response and the predictors across different distance thresholds. Low Moran’s I and p-values equal to or larger than 0.05 indicate that there is no spatial autocorrelation for the given variable and distance threshold.

spatialRF::plot_training_df_moran(
  data = plants_df,
  dependent.variable.name = plants_response,
  predictor.variable.names = plants_predictors,
  distance.matrix = plants_distance,
  distance.thresholds = distance_thresholds,
  fill.color = colors
)

Finding promising variable interactions

The function the_feature_engineer() tests all possible interactions between the most important predictors, and selects the most promising ones via spatial cross-validation (see rf_evaluate()).

interactions <- spatialRF::the_feature_engineer(
  data = plants_df,
  dependent.variable.name = plants_response,
  predictor.variable.names = plants_predictors,
  xy = plants_xy,
  cluster = cluster,
  point.color = colors,
  verbose = TRUE
  )
#>  ┌──────────────────┬──────────────────┬──────────────────┬──────────────────┐
#>  │ Interaction      │ Importance (% of │        R-squared │     Max cor with │
#>  │                  │             max) │      improvement │       predictors │
#>  ├──────────────────┼──────────────────┼──────────────────┼──────────────────┤
#>  │ human_population │            100.0 │            0.039 │             0.64 │
#>  │ ..x..bias_area_k │                  │                  │                  │
#>  │ m2               │                  │                  │                  │
#>  ├──────────────────┼──────────────────┼──────────────────┼──────────────────┤
#>  │ climate_bio1_ave │            100.0 │            0.059 │             0.28 │
#>  │ rage..pca..human │                  │                  │                  │
#>  │ _population      │                  │                  │                  │
#>  ├──────────────────┼──────────────────┼──────────────────┼──────────────────┤
#>  │ climate_bio1_ave │             59.5 │            0.026 │             0.74 │
#>  │ rage..pca..clima │                  │                  │                  │
#>  │ te_hypervolume   │                  │                  │                  │
#>  └──────────────────┴──────────────────┴──────────────────┴──────────────────┘

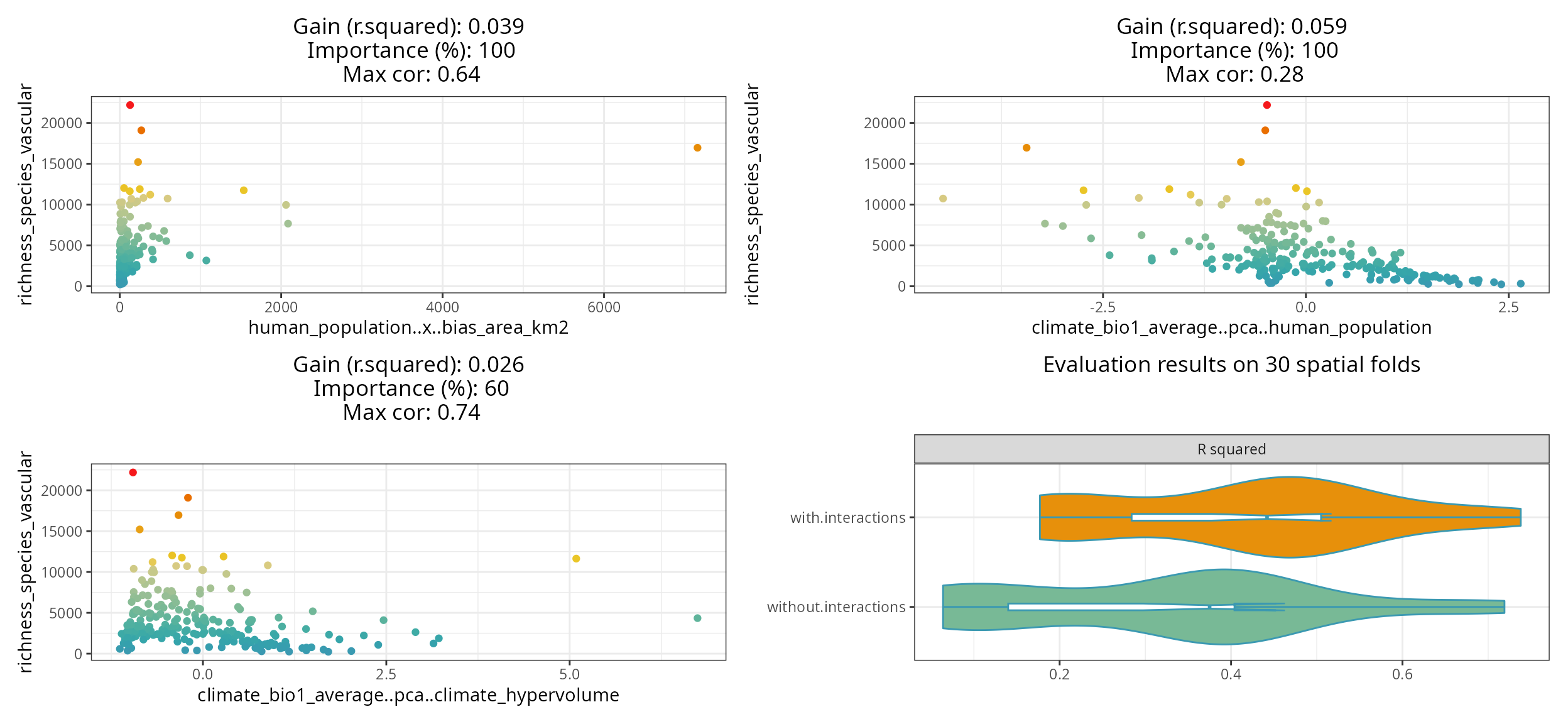
The resulting plot shows the selected interactions against the response, the model improvement they produce, their importance relative to the other predictors, and maximum correlation with the other predictors.

The violin-plot shows the cross-validation comparison of the model with and without the selected interactions.

The function also returns a data frame with the complete screening results.

interaction.name	interaction.importance	interaction.metric.gain	max.cor.with.predictors	variable.a.name	variable.b.name	selected
human_population..x..bias_area_km2	100.000	0.039	0.6373850	human_population	bias_area_km2	TRUE
climate_bio1_average..pca..human_population	100.000	0.059	0.2800000	climate_bio1_average	human_population	TRUE
climate_bio1_average..pca..human_population_density	92.210	0.053	0.3400000	climate_bio1_average	human_population_density	TRUE
climate_bio1_average..pca..climate_hypervolume	59.510	0.026	0.7400000	climate_bio1_average	climate_hypervolume	TRUE
human_population..pca..climate_hypervolume	78.170	-0.017	0.7200000	human_population	climate_hypervolume	FALSE
climate_hypervolume..pca..bias_area_km2	61.640	-0.012	0.7100000	climate_hypervolume	bias_area_km2	FALSE
climate_hypervolume..x..human_population_density	60.856	-0.012	0.5599486	climate_hypervolume	human_population_density	FALSE
climate_hypervolume..pca..human_population_density	40.980	-0.014	0.7200000	climate_hypervolume	human_population_density	FALSE

#adding interaction column to the training data
plants_df <- interactions$data

#adding interaction name to predictor.variable.names
plants_predictors <- interactions$predictor.variable.names

Training a non-spatial Random Forest model with `rf()`

The function rf() is a convenient wrapper for ranger::ranger() used in every modelling function of the spatialRF package.

m <- spatialRF::rf(
  data = plants_df,
  dependent.variable.name = plants_response,
  predictor.variable.names = plants_predictors,
  distance.matrix = plants_distance,
  distance.thresholds = distance_thresholds,
  verbose = FALSE
)

The resulting object has its own print() method.

m
#> Model type
#>   - Fitted with:                     ranger()
#>   - Response variable:               richness_species_vascular
#> 
#> Random forest parameters
#>   - Type:                            Regression
#>   - Number of trees:                 500
#>   - Sample size:                     227
#>   - Number of predictors:            20
#>   - Mtry:                            4
#>   - Minimum node size:               5
#> 
#> 
#> Model performance 
#>   - R squared (oob):                  0.5824533
#>   - R squared (cor(obs, pred)^2):     0.9496391
#>   - Pseudo R squared (cor(obs, pred)):0.9744943
#>   - RMSE (oob):                       2177.649
#>   - RMSE:                             943.1657
#>   - Normalized RMSE:                  0.2722765
#> 
#> Model residuals 
#>   - Stats: 
#>           ┌──────────┬─────────┬─────────┬────────┬────────┬─────────┐
#>           │ Min.     │ 1st Q.  │ Median  │ Mean   │ 3rd Q. │ Max.    │
#>           ├──────────┼─────────┼─────────┼────────┼────────┼─────────┤
#>           │ -2060.04 │ -448.37 │ -140.69 │ -22.32 │ 126.72 │ 7957.63 │
#>           └──────────┴─────────┴─────────┴────────┴────────┴─────────┘
#>   - Normality: 
#>       - Shapiro-Wilks W: 0.745 
#>       - p-value        : 0 
#>       - Interpretation : Residuals are not normal 
#> 
#>   - Spatial autocorrelation: 
#>              ┌──────────┬───────────┬─────────┬──────────────────┐
#>              │ Distance │ Moran's I │ P value │ Interpretation   │
#>              ├──────────┼───────────┼─────────┼──────────────────┤
#>              │     10.0 │     0.116 │   0.000 │ Positive spatial │
#>              │          │           │         │ correlation      │
#>              ├──────────┼───────────┼─────────┼──────────────────┤
#>              │    100.0 │     0.086 │   0.003 │ Positive spatial │
#>              │          │           │         │ correlation      │
#>              ├──────────┼───────────┼─────────┼──────────────────┤
#>              │   1000.0 │     0.049 │   0.000 │ Positive spatial │
#>              │          │           │         │ correlation      │
#>              ├──────────┼───────────┼─────────┼──────────────────┤
#>              │   2000.0 │     0.010 │   0.134 │ No spatial       │
#>              │          │           │         │ correlation      │
#>              ├──────────┼───────────┼─────────┼──────────────────┤
#>              │   4000.0 │    -0.003 │   0.833 │ No spatial       │
#>              │          │           │         │ correlation      │
#>              ├──────────┼───────────┼─────────┼──────────────────┤
#>              │   8000.0 │    -0.005 │   0.707 │ No spatial       │
#>              │          │           │         │ correlation      │
#>              └──────────┴───────────┴─────────┴──────────────────┘
#> 
#> Variable importance: 
#>              ┌──────────────────────────────────────┬────────────┐
#>              │ Variable                             │ Importance │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ human_population                     │   1606.763 │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ climate_bio1_average..pca..human_pop │   1589.018 │
#>              │ ulation                              │            │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ human_population..x..bias_area_km2   │   1538.721 │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ climate_bio1_average                 │   1513.792 │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ climate_hypervolume                  │   1366.092 │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ human_population_density             │   1123.270 │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ bias_area_km2                        │    956.780 │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ climate_bio1_average..pca..climate_h │    939.333 │
#>              │ ypervolume                           │            │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ human_footprint_average              │    903.505 │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ bias_species_per_record              │    849.638 │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ neighbors_count                      │    720.309 │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ neighbors_area                       │    673.171 │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ topography_elevation_average         │    652.118 │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ neighbors_percent_shared_edge        │    601.785 │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ climate_velocity_lgm_average         │    592.276 │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ climate_aridity_index_average        │    562.847 │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ fragmentation_cohesion               │    538.228 │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ climate_bio15_minimum                │    350.787 │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ landcover_herbs_percent_average      │    277.984 │
#>              ├──────────────────────────────────────┼────────────┤
#>              │ fragmentation_division               │    233.688 │
#>              └──────────────────────────────────────┴────────────┘

The output is a list with several slots containing the information required to interpret the model.

names(m)
#>  [1] "predictions"               "num.trees"                
#>  [3] "num.independent.variables" "mtry"                     
#>  [5] "min.node.size"             "variable.importance"      
#>  [7] "variable.importance.local" "prediction.error"         
#>  [9] "forest"                    "splitrule"                
#> [11] "treetype"                  "r.squared"                
#> [13] "call"                      "importance.mode"          
#> [15] "num.samples"               "replace"                  
#> [17] "dependent.variable.name"   "max.depth"                
#> [19] "ranger.arguments"          "importance"               
#> [21] "performance"               "residuals"

The information available in these slots can be plotted (functions named plot_...()), printed (print_...()), or extracted for further analyses (get_...()).

Residuals

The object residuals (m$residuals) stores the normality and spatial autocorrelation tests.

spatialRF::plot_residuals_diagnostics(
  m,
  verbose = FALSE,
  point.color = colors,
  fill.color = colors[1]
  )

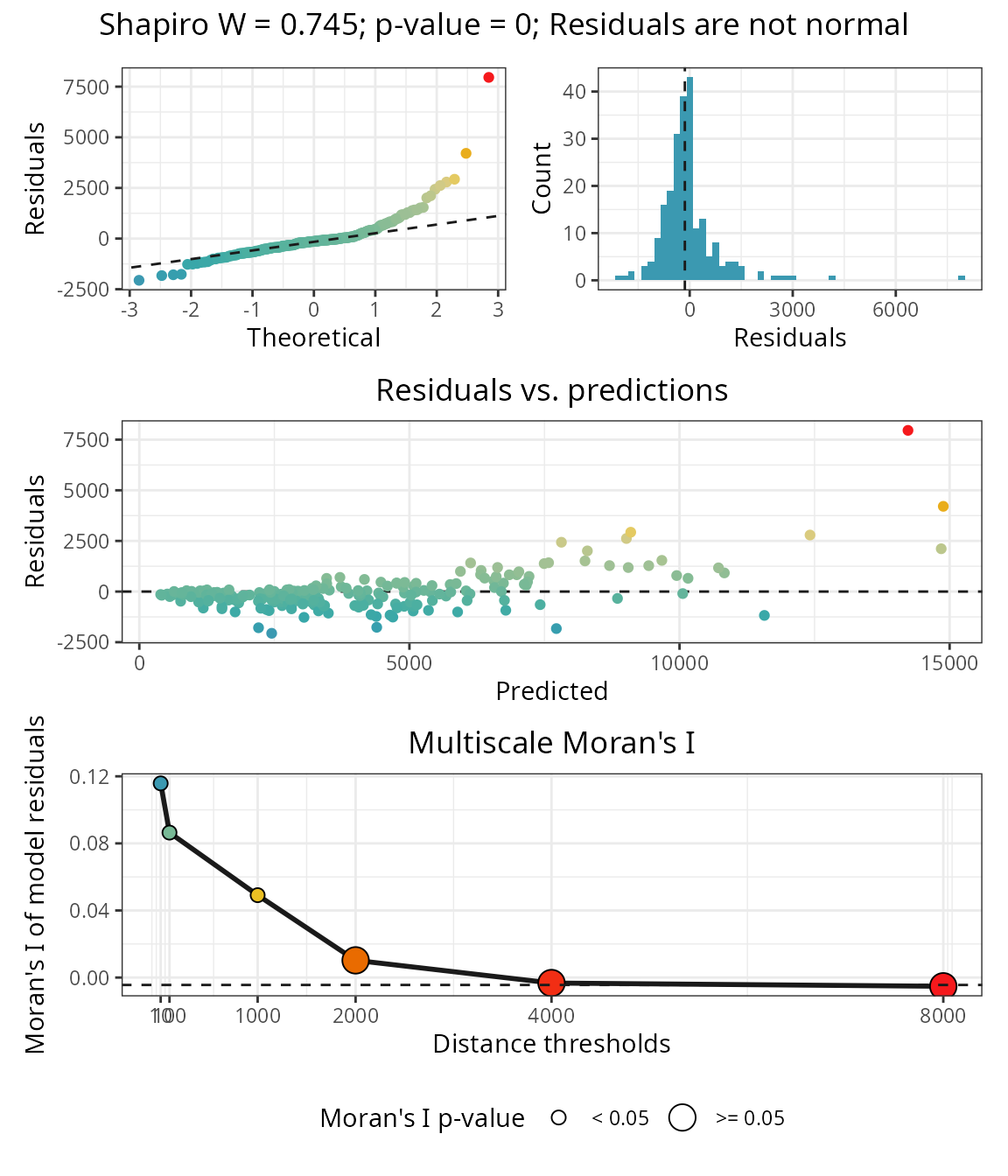The plot show that the residuals are highly correlated up to a point between 1000 and 2000 km between observations, indicating that there is a component of the response not explained by the current predictors.

Variable importance

Global variable importance

The object importance in m$importance) contains the variable importance scores. These can be plotted with plot_importance(), printed with print_importance(), and the dataframe retrieved with get_importance()

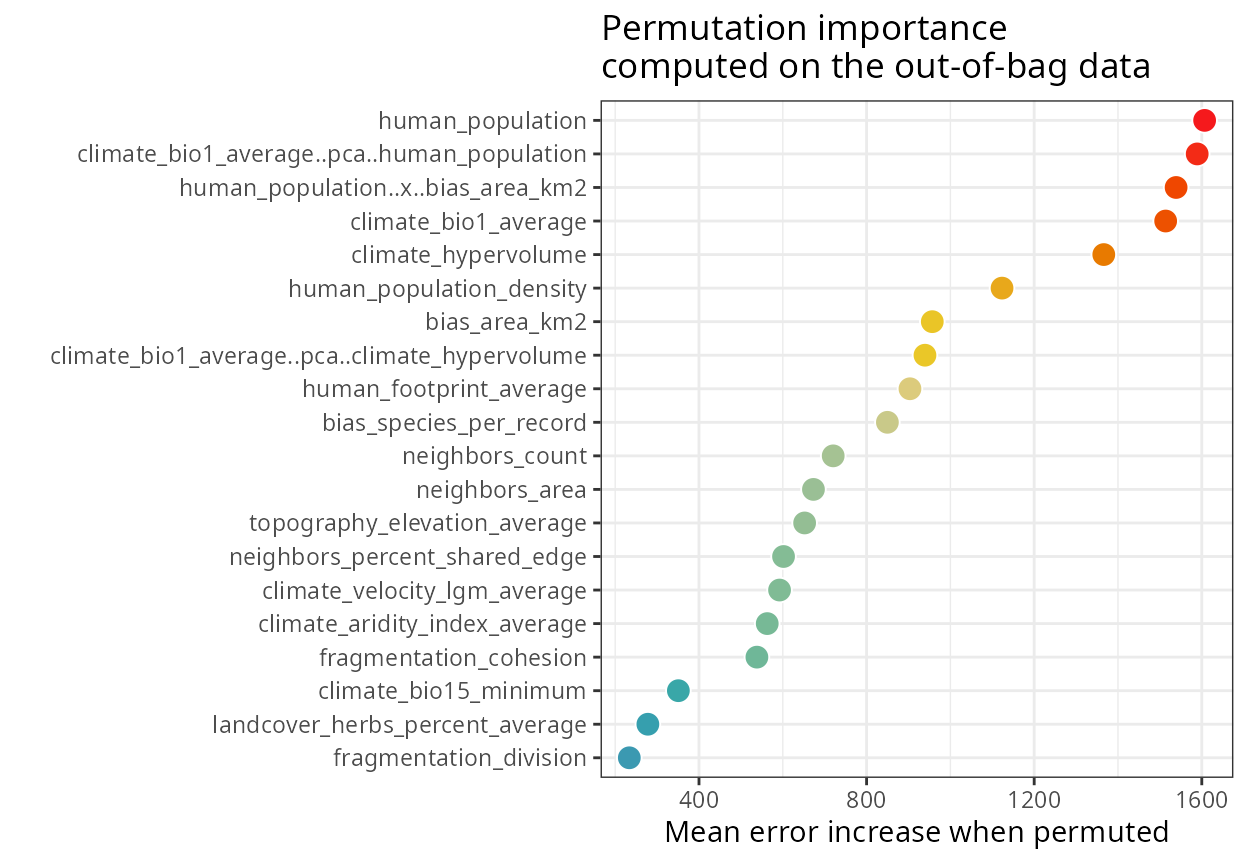
spatialRF::plot_importance(
  m,
  verbose = FALSE,
  fill.color = colors
  )

The output of rf() is also compatible with randomForestExplainer::measure_importance(), which helps deepen our understanding on variable importance scores.

importance.df <- randomForestExplainer::measure_importance(
  m,
  measures = c(
    "mean_min_depth", 
    "no_of_nodes", 
    "times_a_root", 
    "p_value"
    )
  )

variable	mean_min_depth	no_of_nodes	times_a_root	p_value
bias_area_km2	4.01	1800	13	0.95
bias_species_per_record	3.60	2374	5	0.00
climate_aridity_index_average	4.36	1809	4	0.92
climate_bio1_average	2.88	2096	60	0.00
climate_bio1_average..pca..climate_hypervolume	3.79	1821	25	0.86
climate_bio1_average..pca..human_population	2.60	2136	77	0.00
climate_bio15_minimum	4.78	1661	0	1.00
climate_hypervolume	2.98	2091	45	0.00
climate_velocity_lgm_average	4.24	1866	11	0.51
fragmentation_cohesion	4.50	1578	14	1.00
fragmentation_division	5.18	1552	1	1.00
human_footprint_average	4.47	1672	8	1.00
human_population	2.83	2072	65	0.00
human_population_density	3.46	1877	34	0.41
human_population..x..bias_area_km2	2.87	2021	90	0.00
landcover_herbs_percent_average	4.72	1787	0	0.97
neighbors_area	4.37	1722	1	1.00
neighbors_count	3.48	1598	40	1.00
neighbors_percent_shared_edge	4.05	1881	7	0.37
topography_elevation_average	3.92	1922	0	0.10

Contribution of predictors to model transferability

The function rf_importance() assesses how each predictor contributes to model transferability by combining leave-one-predictor-out with spatial cross-validation, and comparing a model trained with the given predictor with a model trained with all other predictors.

m <- spatialRF::rf_importance(
  model = m,
  xy = plants_xy, #needs coordinates for cross-validation
  cluster = cluster,
  fill.color = colors
  )

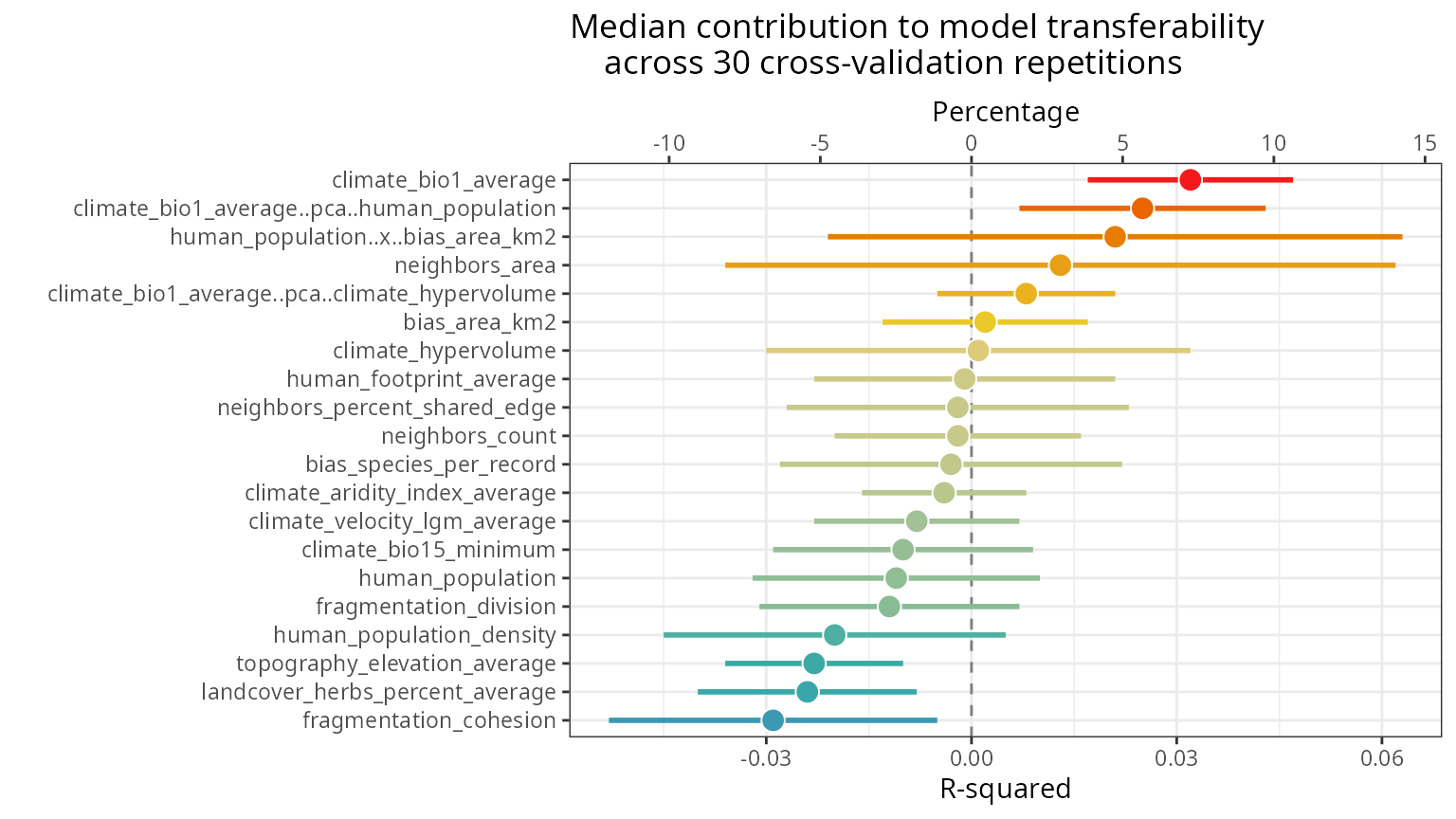The values in the plot are added as new columns with the suffix .cv in the dataframe m$importance$per.variable.

variable	importance.oob	importance.cv	importance.cv.mad	importance.cv.percent	importance.cv.percent.mad
human_population	1606.763	-0.011	0.021	-2.5	7.3
climate_bio1_average..pca..human_population	1589.018	0.025	0.018	5.7	6.3
human_population..x..bias_area_km2	1538.721	0.021	0.042	4.8	14.6
climate_bio1_average	1513.792	0.032	0.015	7.2	5.2
climate_hypervolume	1366.092	0.001	0.031	0.2	11.0
human_population_density	1123.270	-0.020	0.025	-4.5	8.9
bias_area_km2	956.780	0.002	0.015	0.5	5.2
climate_bio1_average..pca..climate_hypervolume	939.333	0.008	0.013	1.8	4.7
human_footprint_average	903.505	-0.001	0.022	-0.2	7.8
bias_species_per_record	849.638	-0.003	0.025	-0.7	8.9
neighbors_count	720.309	-0.002	0.018	-0.5	6.3
neighbors_area	673.171	0.013	0.049	2.9	17.2
topography_elevation_average	652.118	-0.023	0.013	-5.2	4.7
neighbors_percent_shared_edge	601.785	-0.002	0.025	-0.5	8.9
climate_velocity_lgm_average	592.276	-0.008	0.015	-1.8	5.2
climate_aridity_index_average	562.847	-0.004	0.012	-0.9	4.2
fragmentation_cohesion	538.228	-0.029	0.024	-6.6	8.4
climate_bio15_minimum	350.787	-0.010	0.019	-2.3	6.8
landcover_herbs_percent_average	277.984	-0.024	0.016	-5.4	5.7
fragmentation_division	233.688	-0.012	0.019	-2.7	6.8

Local variable importance

The rf() function computes local importance as a case-by-case average increase in error when a predictor is permuted.

The dataframe of local importance, stored at m$importance$local, can be retrieved with get_importance_local() to create a local importance map.

local.importance <- cbind(
  plants_xy,
  spatialRF::get_importance_local(m)
  )

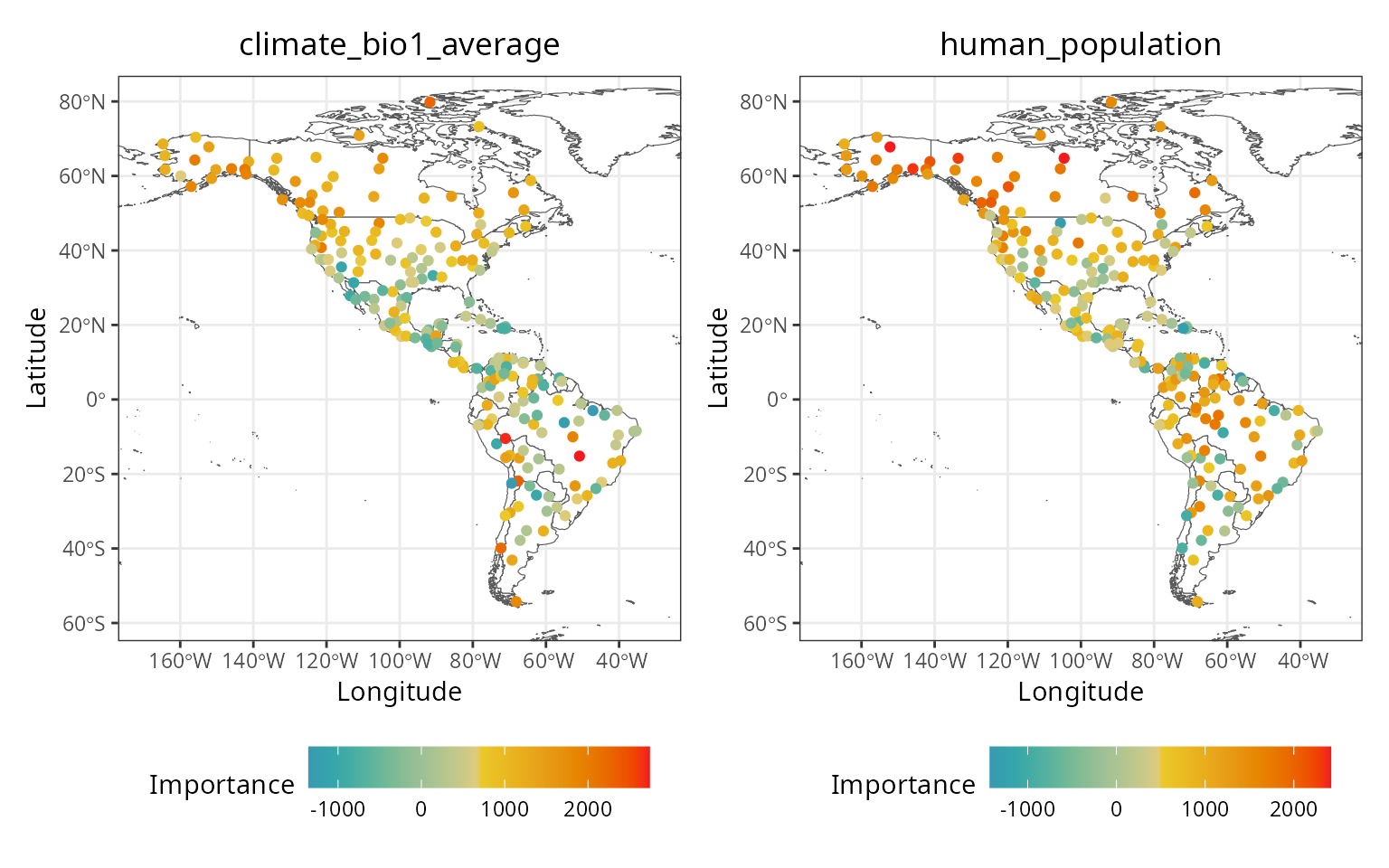
In these maps, a value lower than 0 indicates that the influence of the predictor on the local prediction is worse than what is expected by chance.

Response curves and surfaces

The response curve of a predictor is computed by setting the other predictors to a given quantile (0.1, 0.5, and 0.9 by default).

spatialRF::plot_response_curves(
  m,
  quantiles = c(0.1, 0.5, 0.9),
  line.color = colors[c(1, 50, 100)],
  ncol = 3,
  show.data = FALSE
  )

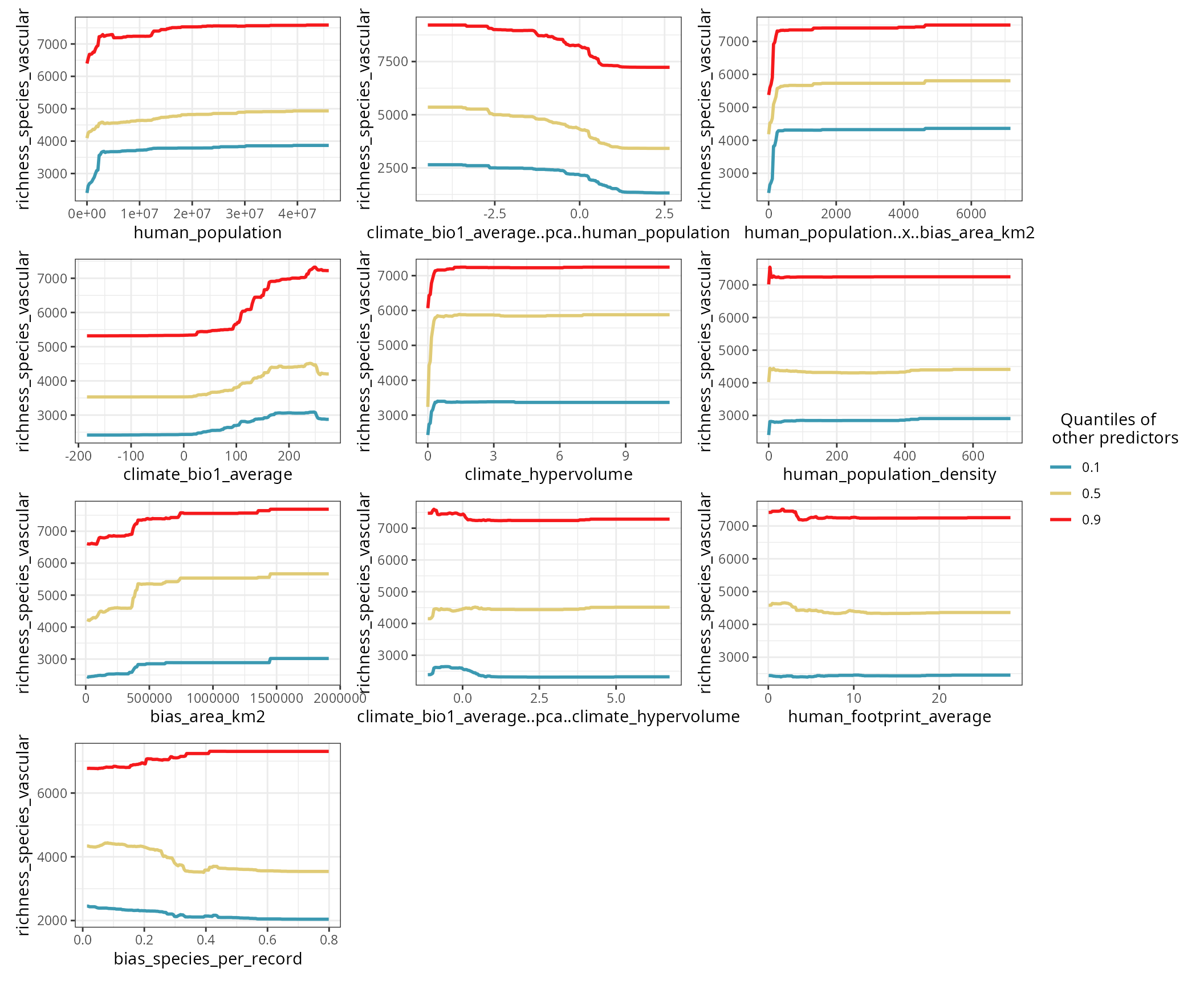
The blue curve (quantile 0.1) shows the point estimate for a predictor when all other predictors are at their lowest values.

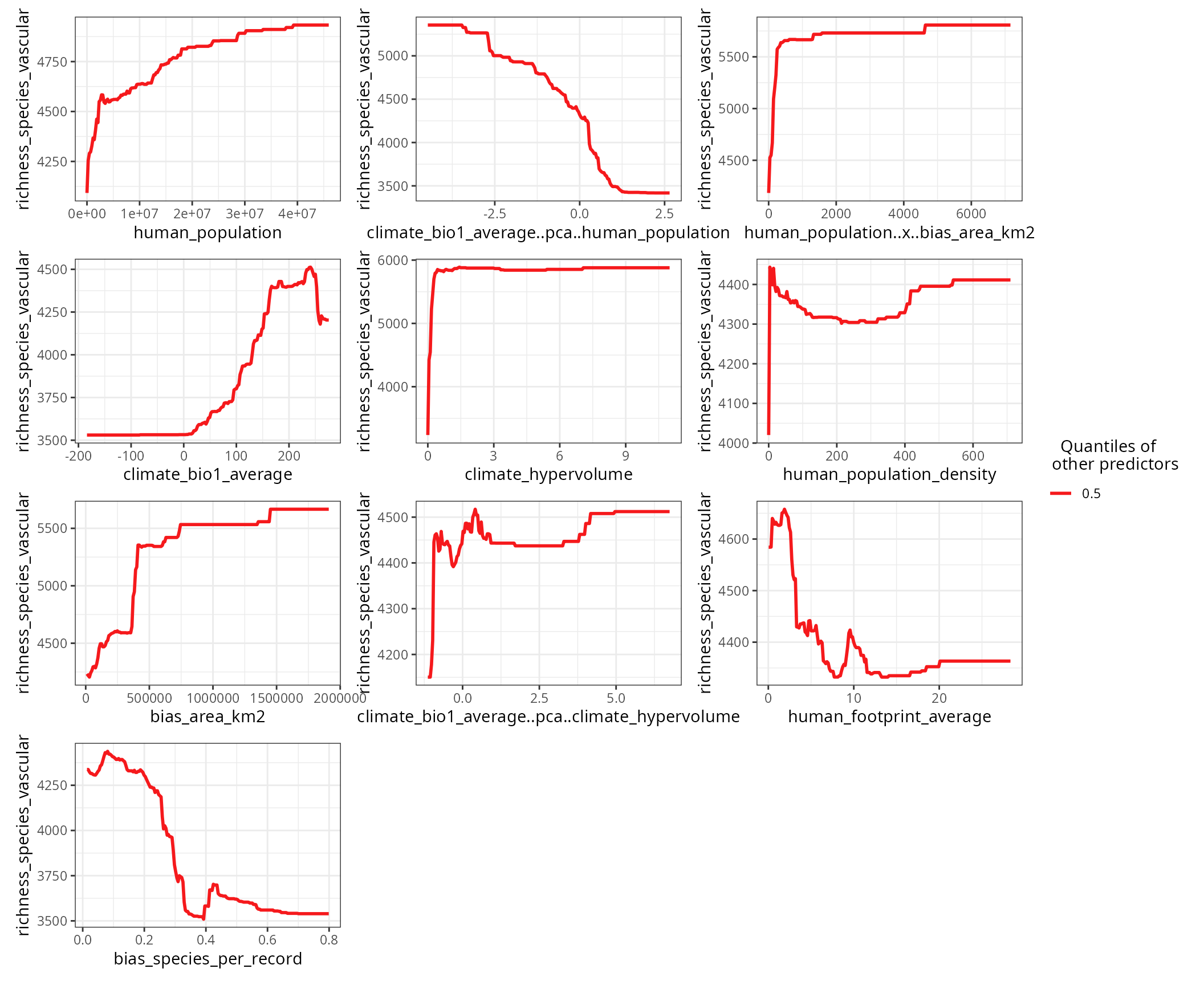
Setting the argument quantiles to 0.5 and setting show.data to FALSE (default option) accentuates the shape of the response curves.

spatialRF::plot_response_curves(
  m,
  quantiles = 0.5,
  line.color = colors[100],
  ncol = 3
  )

If you need to do your own plots, the function get_response_curves() returns a data frame with the required data.

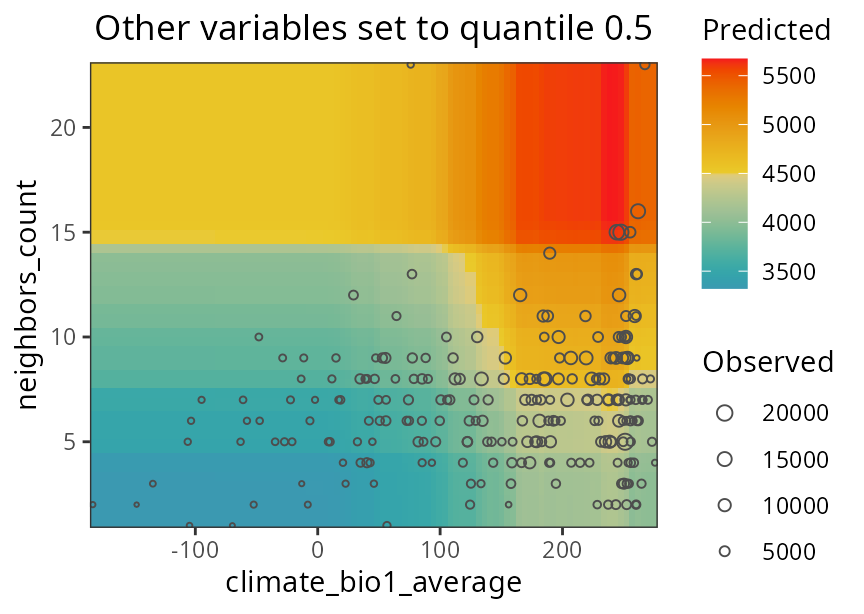
response.curves.df <- spatialRF::get_response_curves(m)

Interactions between two predictors can be plotted with plot_response_surface().

spatialRF::plot_response_surface(
  model = m,
  a = "climate_bio1_average",
  b = "neighbors_count",
  fill.color = colors
  )

Performance

The performance slot, stored at m$performance, contains the values of several performance measures. It be printed via the function print_performance().

spatialRF::print_performance(m)
#> 
#> Model performance 
#>   - R squared (oob):                  0.5824533
#>   - R squared (cor(obs, pred)^2):     0.9496391
#>   - Pseudo R squared (cor(obs, pred)):0.9744943
#>   - RMSE (oob):                       2177.649
#>   - RMSE:                             943.1657
#>   - Normalized RMSE:                  0.2722765

R squared (oob) and RMSE (oob) are computed by ranger::ranger() on the out-of-bag data (fraction of data not used to train individual trees). From all the values available in the performance slot, these are probably the most honest ones. However, out-of-bag data is not fully independent, and therefore will still be inflated, especially if the data is highly aggregated in space.
R squared and pseudo R squared are computed from comparing all observations against predictions. These values will usually be high when spatial autocorrelation is high.
The RMSE and its normalized version are linear with R squared and pseudo R squared.

Hyperparameter tuning

The function rf_tuning() optimizes the values for three critical Random Forest hyperparameters via spatial cross-validation:

num.trees: number of regression trees in the forest.
mtry: number of variables to choose from on each tree split.
min.node.size: minimum number of cases on a terminal node.

m <- rf_tuning(
  model = m,
  xy = plants_xy,
  repetitions = 30,
  num.trees = c(100, 200, 300),
  mtry = c(2, 4, 8),
  min.node.size = c(5, 10, 20),
  cluster = cluster,
  verbose = TRUE
)

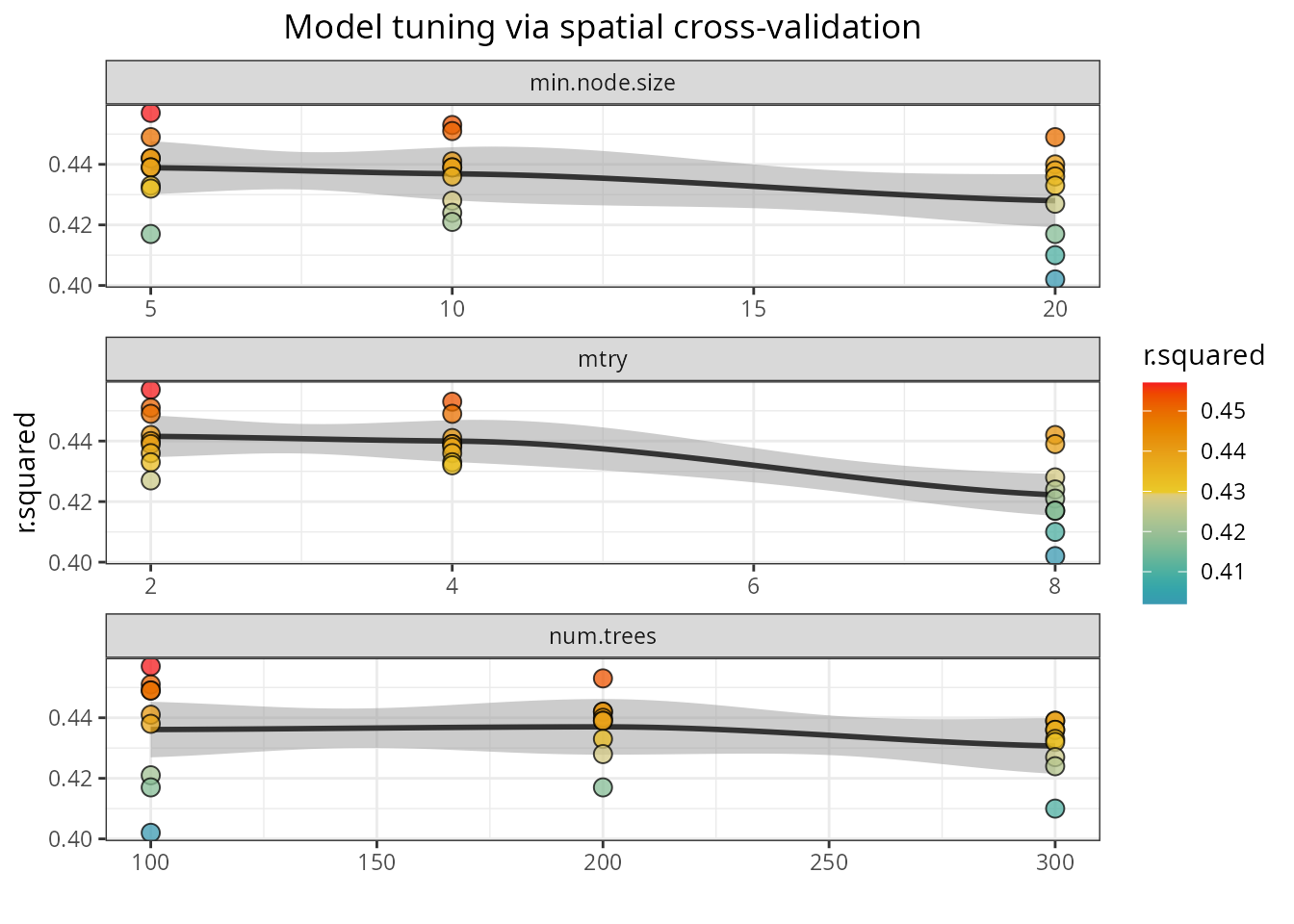
The function returns a tuned model only if the tuning finds a solution better than the original model. The tuning results can be accessed with plot_tuning().

spatialRF::plot_tuning(
  model = m,
  point.color = colors
)

Spatial cross-validation

The function rf_evaluate() provides honest performance scores based on spatial cross-validation. The function separates the data into spatially independent training and testing folds.

m <- spatialRF::rf_evaluate(
  model = m,
  xy = plants_xy,           #data coordinates
  repetitions = 30,         #number of spatial folds
  training.fraction = 0.75, #training data fraction on each fold
  metrics = "r.squared",
  cluster = cluster,
  verbose = FALSE
)

The function creates m$evaluation with several objects that summarize the spatial cross-validation results.

names(m$evaluation)
#> [1] "metrics"           "training.fraction" "spatial.folds"    
#> [4] "per.fold"          "per.fold.long"     "per.model"        
#> [7] "aggregated"

The slot “spatial.folds”, produced by make_spatial_folds(), contains the indices of the training and testing cases for each cross-validation repetition. The maps below show two sets of training and testing folds.

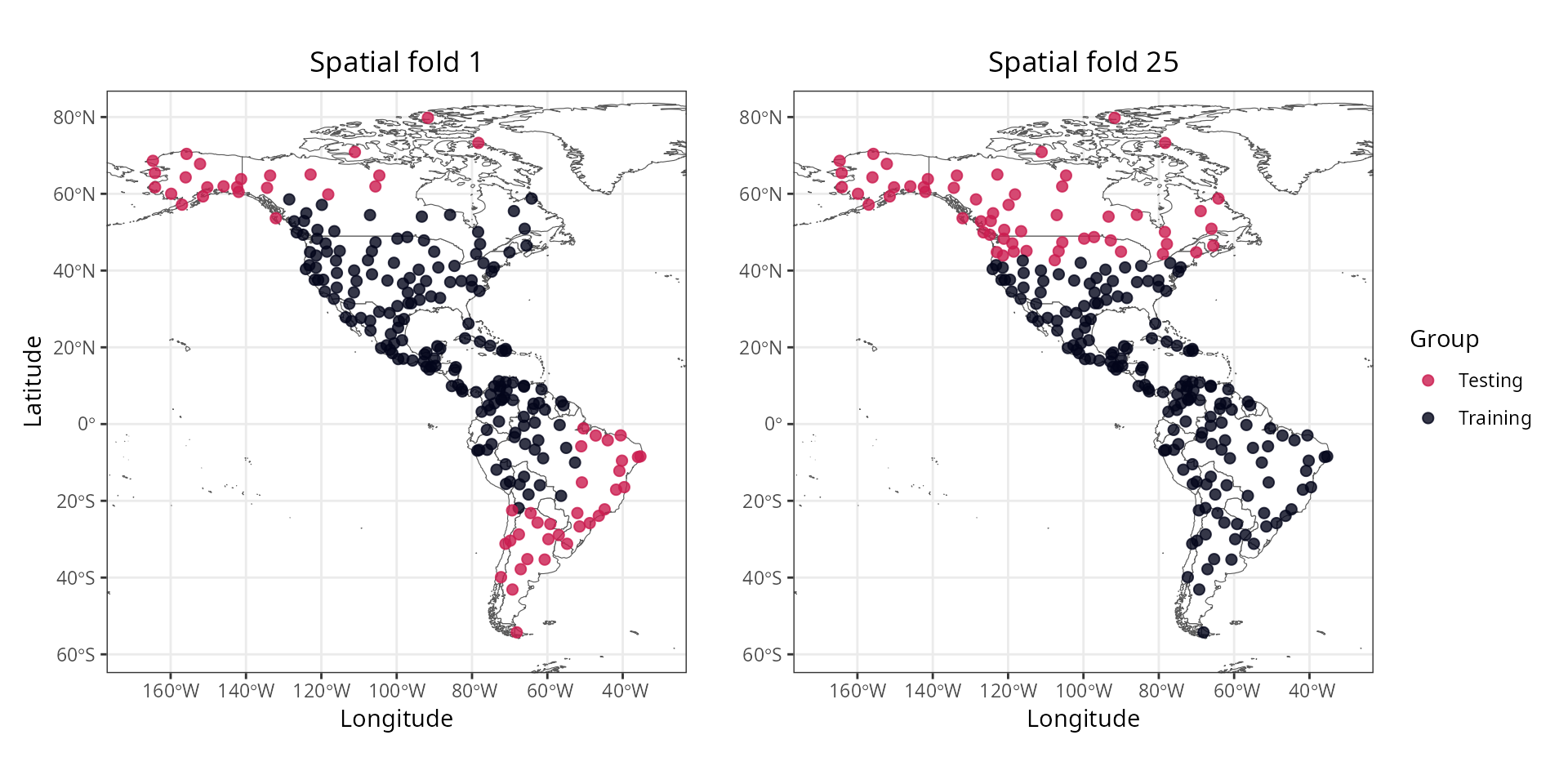
The information available in this new slot can be accessed with the functions print_evaluation(), plot_evaluation(), and get_evaluation().

spatialRF::plot_evaluation(
  model = m,
  fill.color = colors,
  notch = FALSE
  )

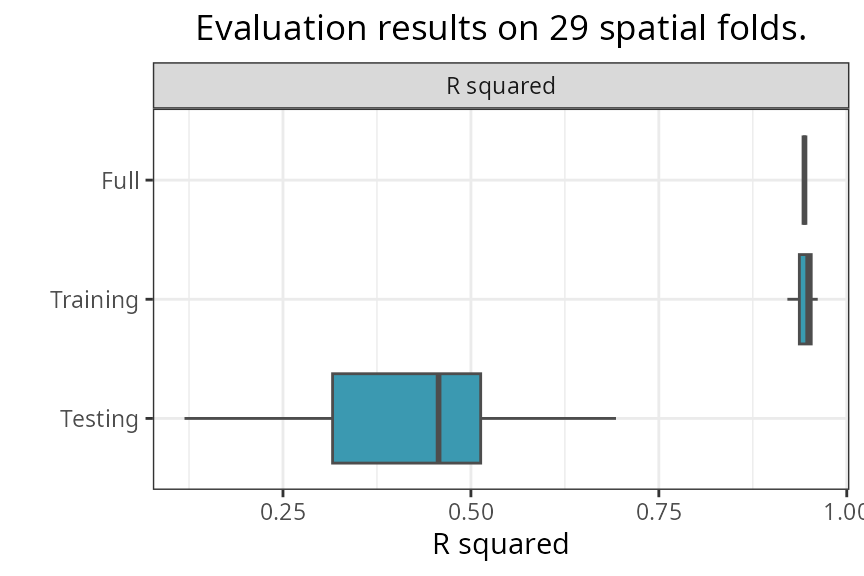
Full is the performance of the model trained on the full dataset.
Training is the performance of the model trained on the training folds.
Testing is the performance of the model on the testing folds.

The median, median absolute deviation (MAD), minimum, and maximum R-squared values on the testing folds can be printed with print_evaluation().

spatialRF::print_evaluation(m)
#> 
#> Spatial evaluation 
#>   - Training fraction:             0.75
#>   - Spatial folds:                 29
#> 
#>     Metric Median   MAD Minimum Maximum
#>  r.squared  0.457 0.136   0.119   0.693

Prediction

Models trained with rf() can be predicted as follows.

predicted <- predict(
  object = m,
  data = plants_df,
  type = "response"
  )$predictions

head(predicted)
#> [1]  5100.050  4528.267  1569.679  7188.758 11608.656  2640.325

Next steps

This tutorial covered non-spatial random forest modeling. To learn how to address spatial autocorrelation in model residuals using spatial predictors, see the Spatial Random Forest Models tutorial.