Spatial Random Forest Models • spatialRF

Introduction

This tutorial demonstrates how to address spatial autocorrelation in random forest model residuals using the spatialRF package. Spatial autocorrelation occurs when model residuals at nearby locations are more similar than expected by chance, violating the assumption of independence and potentially leading to inflated performance metrics and biased variable importance scores.

The rf_spatial() function addresses this issue by incorporating spatial predictors (Moran’s Eigenvector Maps) that capture spatial structure not explained by environmental predictors alone.

For an introduction to non-spatial random forest modeling with spatialRF, see the Non-Spatial Random Forest Models tutorial.

Setup

library(spatialRF)
library(ggplot2)
library(dplyr)
library(rnaturalearth)
library(rnaturalearthdata)
library(parallel)
library(patchwork)
library(tidyr)

# Load data and precomputed non-spatial model
data(
  plants_df,
  plants_response,
  plants_predictors,
  plants_distance,
  plants_xy,
  plants_rf  # precomputed non-spatial model
)

#distance thresholds (same units as plants_distance, km)
#used to assess spatial correlation at different distances
distance_thresholds <- c(10, 100, 1000, 2000, 4000, 8000)

#a pretty color palette
colors <- grDevices::hcl.colors(
    n = 100,
    palette = "Zissou 1"
    )

# Parallel backend
cluster <- parallel::makeCluster(
  parallel::detectCores() - 1,
  type = "PSOCK"
)

# Load world map for visualizations
world <- rnaturalearth::ne_countries(
  scale = "medium",
  returnclass = "sf"
)

Non-spatial vs spatial model

The plot below shows the spatial autocorrelation of of the residuals from a non-spatial model.

m.non_spatial <- spatialRF::rf(
  data = plants_df,
  dependent.variable.name = plants_response,
  predictor.variable.names = plants_predictors,
  distance.matrix = plants_distance,
  distance.thresholds = distance_thresholds,
  verbose = FALSE
)

spatialRF::plot_moran(
  model = m.non_spatial,
  verbose = FALSE,
  point.color = colors
  )

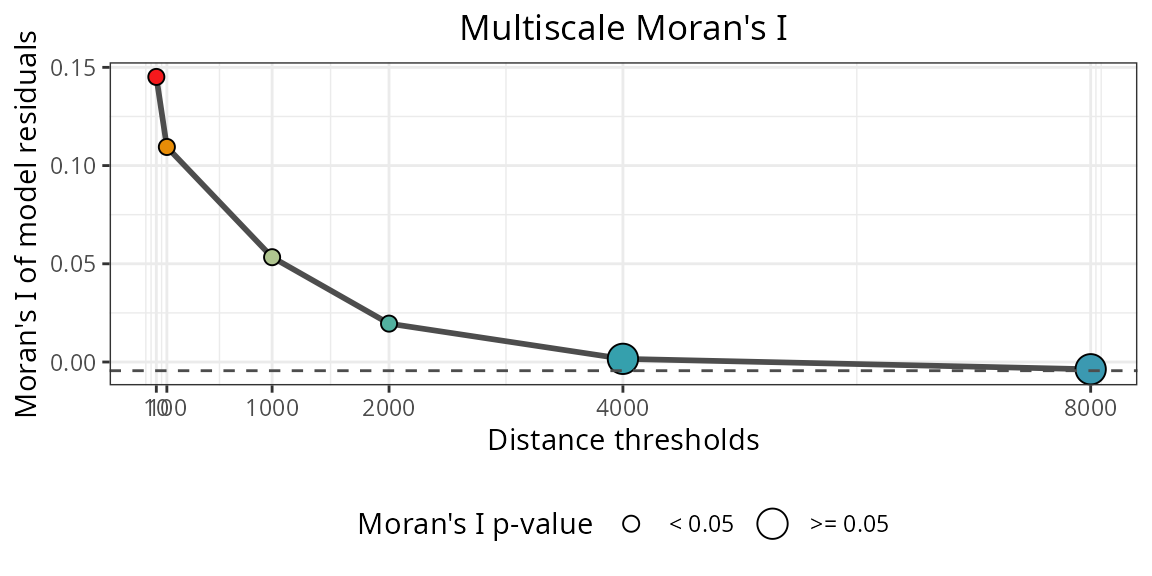
The spatial autocorrelation of the model residuals is high for neighborhood distances up to ~3000km

To reduce the spatial autocorrelation of the residuals as much as possible, the non-spatial model can be transformed into a spatial model with rf_spatial().

This function is the true core of the package!

m.spatial <- spatialRF::rf_spatial(
  model = m.non_spatial,
  cluster = cluster,
  verbose = FALSE
  )

spatialRF::plot_moran(
  model = m.spatial,
  verbose = FALSE,
  point.color = colors
  )

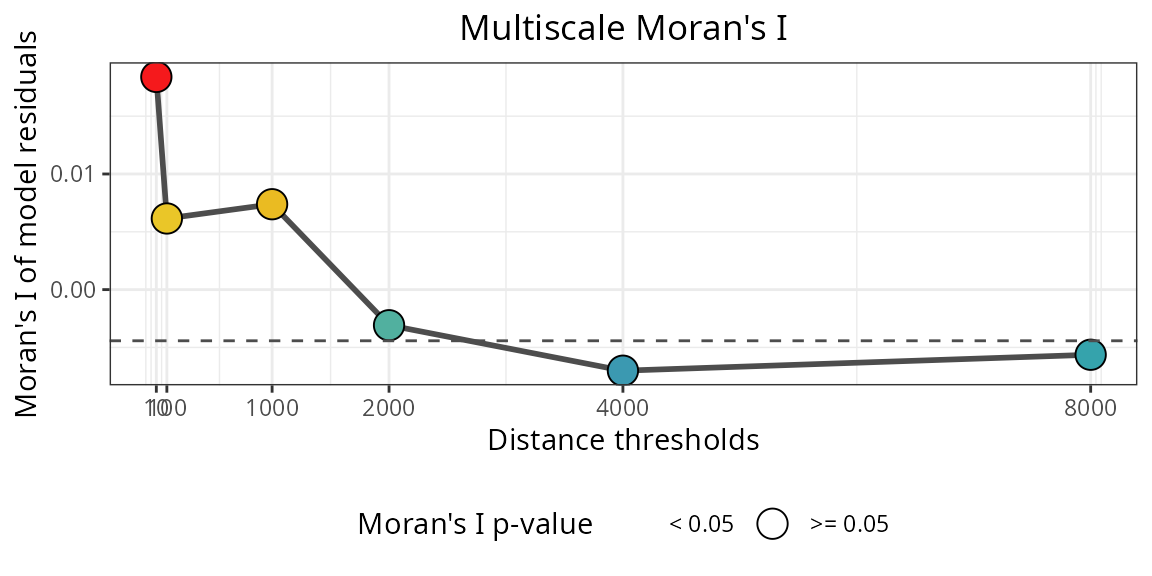
The residuals of the spatial model plotted above are not spatially correlated anymore!

This improvement results from adding spatial predictors to the model.

Spatial predictors

The variable importance plot below shows that the spatial model has spatial predictors with varying levels or importance.

spatialRF::plot_importance(
  model = m.spatial,
  verbose = FALSE,
  fill.color = colors
  )

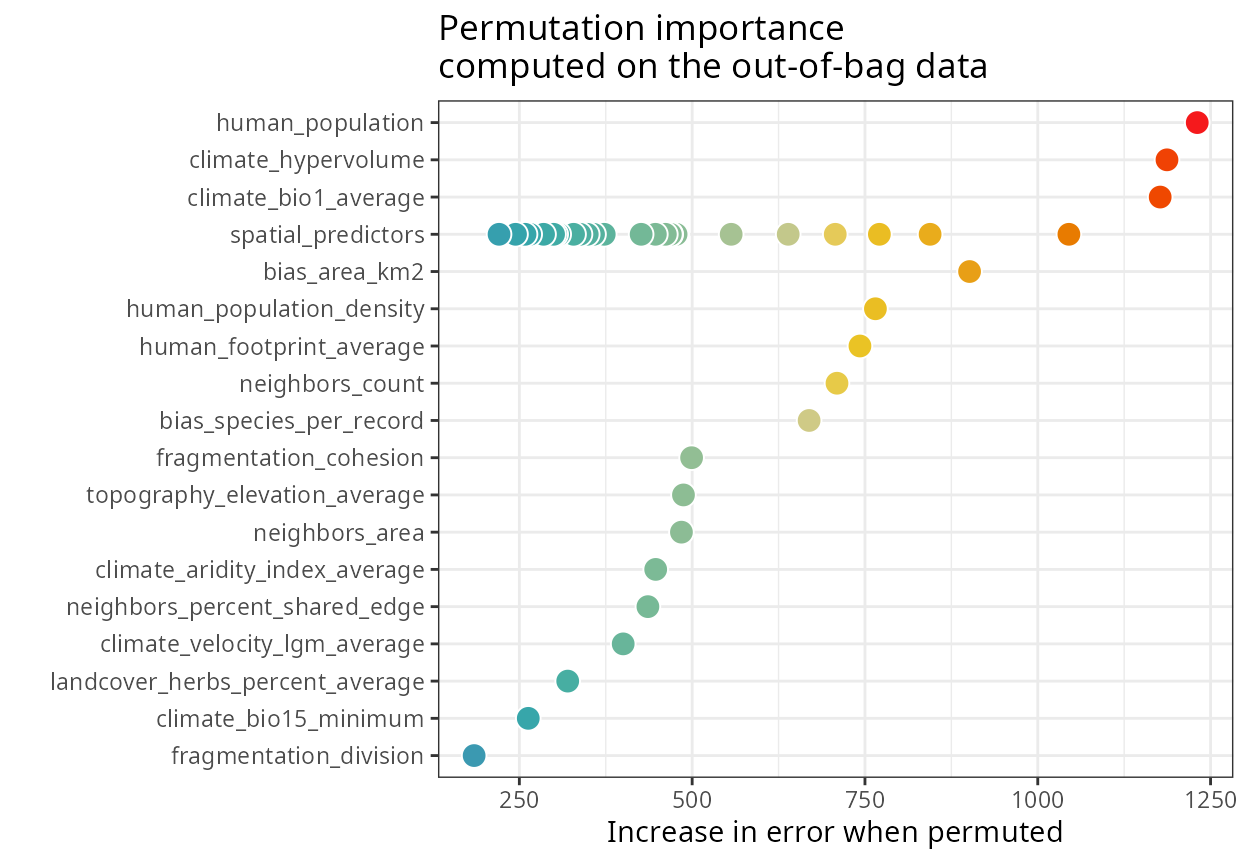
Spatial predictors are named spatial_predictor_X_Y, where X is the neighborhood distance at which the predictor is generated, and Y is the index of the predictor.

variable	importance
spatial_predictor_10_3	1045.043
spatial_predictor_10_2	844.255
spatial_predictor_10_5	770.861
spatial_predictor_10_1	707.001
spatial_predictor_10_4	638.946
spatial_predictor_10_13	556.443
spatial_predictor_10_10	477.876
spatial_predictor_10_20	476.759
spatial_predictor_10_8	468.989
spatial_predictor_10_16	468.463
spatial_predictor_2000_3	461.205
spatial_predictor_10_15	446.738
spatial_predictor_1000_11	426.185
spatial_predictor_10_12	372.793
spatial_predictor_10_17	357.319
spatial_predictor_10_22	348.198
spatial_predictor_10_14	337.736
spatial_predictor_10_11	328.416
spatial_predictor_10_21	306.931
spatial_predictor_10_9	302.574
spatial_predictor_10_7	299.491
spatial_predictor_10_19	285.000
spatial_predictor_10_18	264.969
spatial_predictor_2000_6	258.225
spatial_predictor_1000_9	244.433
spatial_predictor_1000_10	220.619

Spatial predictors are smooth surfaces representing neighborhood among records at different spatial scales. They are computed from the distance matrix in different ways.

The ones computed by default in rf_spatial() are the eigenvectors of the double-centered distance matrix of weights (a.k.a, Moran’s Eigenvector Maps).

They represent the effect of spatial proximity among records, helping to represent biogeographic and spatial processes not considered by the non-spatial predictors.

They can be extracted from the model with the function get_spatial_predictors().

spatial.predictors <- spatialRF::get_spatial_predictors(m.spatial)

The map below shows a couple of them.

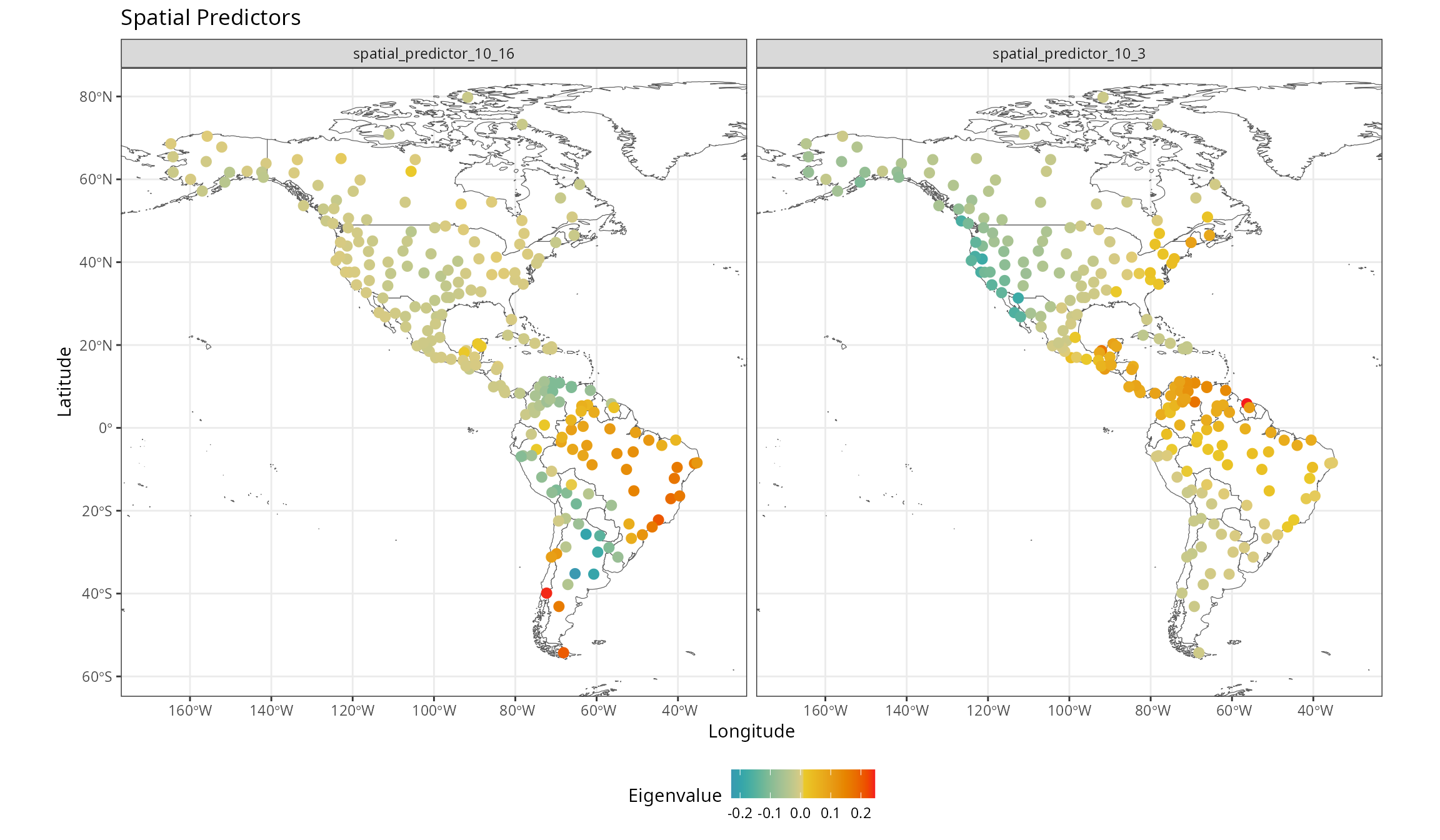
Selection of spatial predictors

The spatial predictors are included in the model sequentially via select_spatial_predictors_sequential(). This function finds the smallest subset of spatial predictors that maximizes the model’s R squared and minimizes the Moran’s I of the residuals.

spatialRF::plot_optimization(
  model = m.spatial,
  point.color = colors
  )

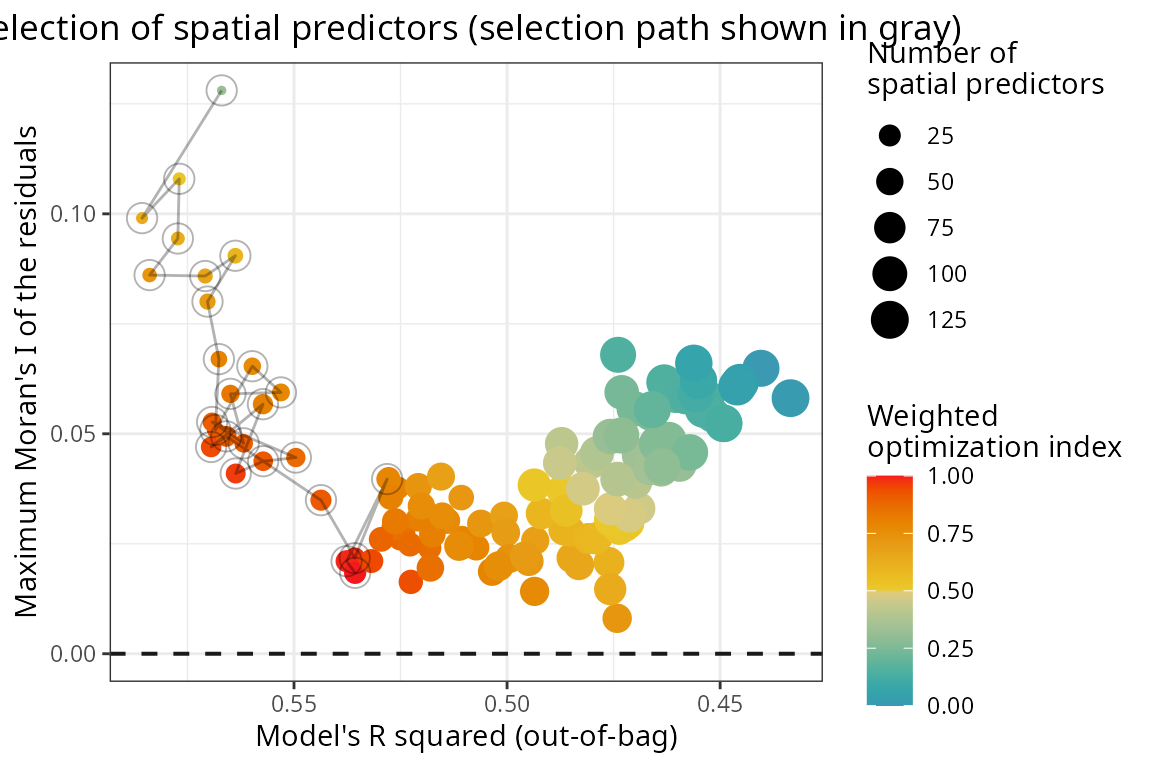The path in the plot below shows the iterative selection of spatial predictors, that tries to reduce the spatial autocorrelation of the residuals (y axis) without degrading model performance (x axis).

Model comparison

The function rf_compare() takes named list with models trained with the same data, and applies rf_evaluate() to each one of them to compare their predictive performances across spatial folds.

comparison <- spatialRF::rf_compare(
  models = list(
    `Non-spatial` = m.non_spatial,
    `Spatial` = m.spatial
  ),
  xy = plants_xy,
  repetitions = 30,
  training.fraction = 0.8,
  fill.color = colors,
  cluster = cluster,
  metrics = "r.squared"
  )

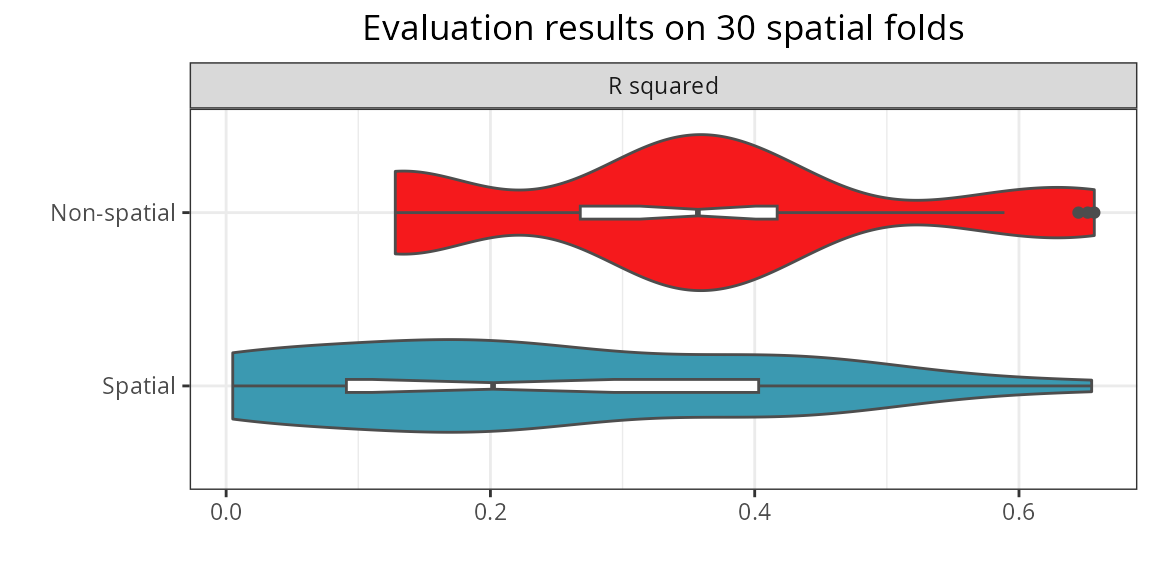
The comparison shows that the spatial model has a better performance on when predicting on independent spatial folds. This is an expected behavior: spatial predictors make models less transferable in space! That’s why spatialRF is focused on explanatory models rather than predictive ones.

Using spatial predictors in other models

Spatial predictors from spatialRF can be used with any modeling method. The workflow: generate MEMs, rank by Moran’s I, add sequentially until residual autocorrelation is resolved.

#generate and rank MEMs
mems <- spatialRF::mem_multithreshold(
  distance.matrix = plants_distance,
  distance.thresholds = distance_thresholds
)

ranked <- spatialRF::rank_spatial_predictors(
  distance.matrix = plants_distance,
  spatial.predictors.df = mems,
  ranking.method = "moran"
)

mems <- mems[, ranked$ranking]

#prepare scaled data
plants_df.scaled <- plants_df |> 
  scale() |> 
  as.data.frame()

#fit non-spatial model
m1 <- lm(
  richness_species_vascular ~ human_population + climate_bio1_average +
    climate_hypervolume + human_footprint_average,
  data = plants_df.scaled
)

#check autocorrelation
m1.moran <- spatialRF::moran(
  x = residuals(m1),
  distance.matrix = plants_distance,
  verbose = FALSE
)

m1.moran$plot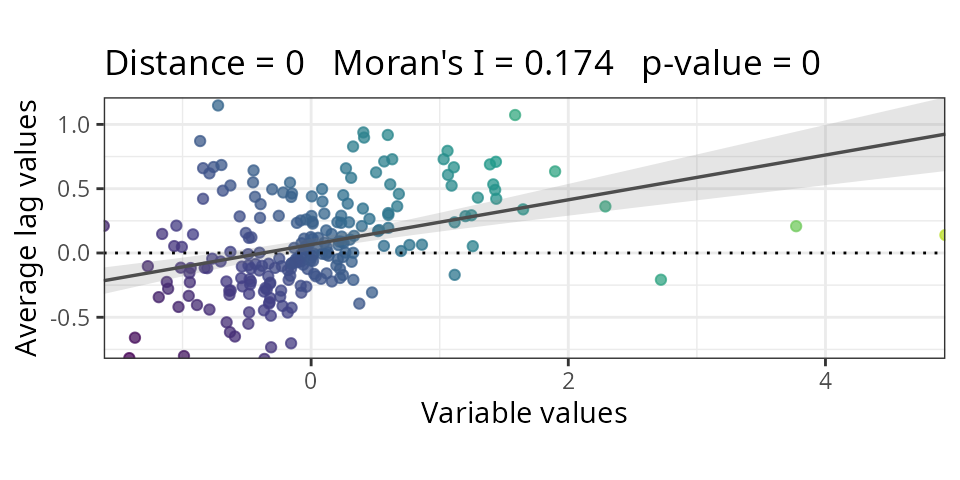

Residuals show spatial autocorrelation. Let’s add MEMs sequentially:

#combine data with MEMs
plants_df.mem <- cbind(plants_df.scaled, mems) |> scale() |> as.data.frame()

#add MEMs until autocorrelation resolved
spatial_predictors <- character(0)

for(i in seq_along(mems)){

  spatial_predictors <- c(spatial_predictors, names(mems)[i])

  formula_i <- reformulate(
    c(
      "human_population", 
      "climate_bio1_average",
      "climate_hypervolume", 
      "human_footprint_average",
      spatial_predictors
      ),
    response = plants_response
  )

  m2 <- lm(
    formula = formula_i, 
    data = plants_df.mem
    )

  m2.moran <- spatialRF::moran(
    x = residuals(m2),
    distance.matrix = plants_distance,
    verbose = FALSE
  )

  if(m2.moran$test$interpretation == "No spatial correlation") break
}

m2.moran$plot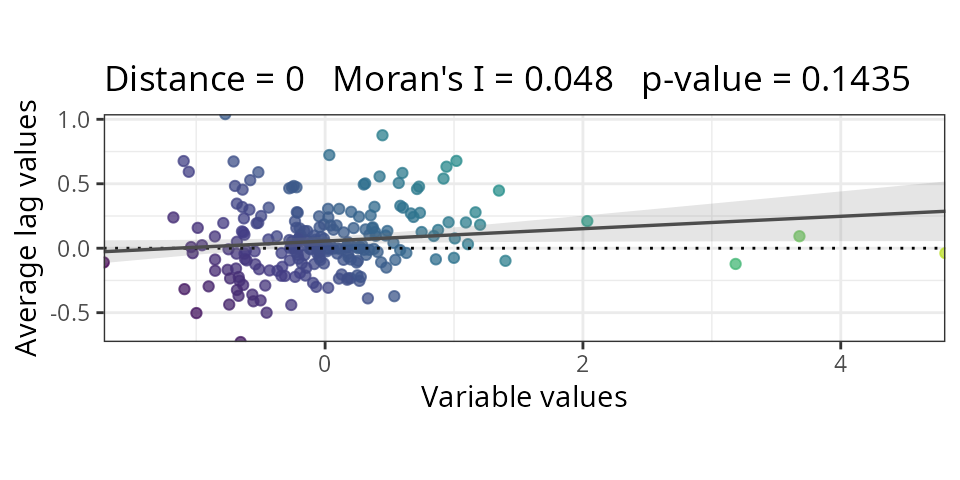

Compare models:

Model	Predictors	R2	Moran_I
Non-spatial	4	0.386	0.174
Spatial	24	0.494	0.048

Adding the spatial predictors eliminated autocorrelation while improving model fit.